Zero-dimensional mapping
A continuous mapping 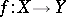 (where
(where 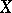 and
and 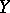 are topological spaces) such that
are topological spaces) such that 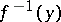 is a zero-dimensional set (in the sense of
is a zero-dimensional set (in the sense of 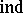 ) for every
) for every 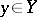 . The application of zero-dimensional and closely related mappings reduces the study of a given space to that of another, simpler, one. Thus, many dimension properties and other cardinal invariants (cf. Cardinal characteristic) transfer from
. The application of zero-dimensional and closely related mappings reduces the study of a given space to that of another, simpler, one. Thus, many dimension properties and other cardinal invariants (cf. Cardinal characteristic) transfer from 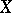 to
to 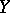 (or, more often, from
(or, more often, from 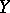 to
to 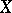 ).
).
Example 1.
Every metric space  with
with  admits a complete zero-dimensional mapping into a space
admits a complete zero-dimensional mapping into a space  with a countable base and
with a countable base and 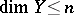 (Katetov's theorem). Here, complete zero-dimensionality means that for every
(Katetov's theorem). Here, complete zero-dimensionality means that for every 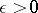 and every
and every  there is a neighbourhood
there is a neighbourhood  whose inverse image
whose inverse image  splits into a discrete system of open sets in
splits into a discrete system of open sets in  of diameter
of diameter 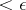 .
.
Example 2.
If a zero-dimensional mapping 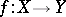 , where
, where 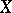 is a normal locally connected space, is a perfect mapping, then the weight of
is a normal locally connected space, is a perfect mapping, then the weight of 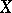 is the same as that of
is the same as that of 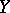 (cf. Weight of a topological space).
(cf. Weight of a topological space).
References
| [1] | P.S. Aleksandrov, B.A. Pasynkov, "Introduction to dimension theory" , Moscow (1973) (In Russian) |
Comments
The starting point for studying zero-dimensional mappings was the theorem in compact metric spaces that if 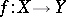 is zero-dimensional, then
is zero-dimensional, then 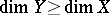 . It extends to separable metric spaces for closed continuous mappings, but not for open ones; see [a1], p. 91.
. It extends to separable metric spaces for closed continuous mappings, but not for open ones; see [a1], p. 91.
References
| [a1] | W. Hurevicz, G. Wallman, "Dimension theory" , Princeton Univ. Press (1948) |
| [a2] | R. Engelking, "General topology" , Heldermann (1989) |
Zero-dimensional mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zero-dimensional_mapping&oldid=43456