Irreducible module
simple module
A non-zero unitary module  over a ring
over a ring 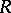 with a unit element that contains only two submodules: the null module and
with a unit element that contains only two submodules: the null module and 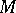 itself.
itself.
Examples. 1) If 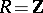 is the ring of integers, then the irreducible
is the ring of integers, then the irreducible 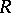 -modules are the Abelian groups of prime order. 2) If
-modules are the Abelian groups of prime order. 2) If 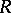 is a skew-field, then the irreducible
is a skew-field, then the irreducible 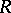 -modules are the one-dimensional vector spaces over
-modules are the one-dimensional vector spaces over  . 3) If
. 3) If 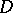 is a skew-field,
is a skew-field, 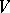 is a left vector space over
is a left vector space over 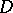 and
and 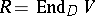 is the ring of linear transformations of
is the ring of linear transformations of 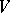 (or a dense subring of it), then the right
(or a dense subring of it), then the right 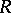 -module
-module 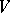 is irreducible. 4) If
is irreducible. 4) If 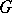 is a group and
is a group and 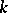 is a field, then the irreducible representations of
is a field, then the irreducible representations of 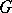 over
over 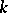 are precisely the irreducible modules over the group algebra
are precisely the irreducible modules over the group algebra 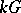 .
.
A right 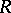 -module
-module 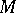 is irreducible if and only if it is isomorphic to
is irreducible if and only if it is isomorphic to 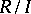 , where
, where 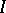 is a maximal right ideal in
is a maximal right ideal in 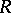 . If
. If 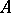 and
and 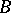 are irreducible
are irreducible  -modules and
-modules and 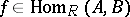 , then either
, then either 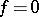 or
or 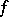 is an isomorphism (which implies that the endomorphism ring of an irreducible module is a skew-field). If
is an isomorphism (which implies that the endomorphism ring of an irreducible module is a skew-field). If 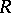 is an algebra over an algebraically closed field and if
is an algebra over an algebraically closed field and if 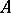 and
and 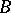 are irreducible modules over
are irreducible modules over 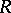 , then (Schur's lemma)
, then (Schur's lemma)
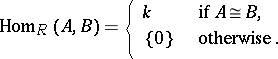 |
The concept of an irreducible module is fundamental in the theories of rings and group representations. By means of it one defines the composition sequence and the socle of a module, the Jacobson radical of a module and of a ring, and a completely-reducible module. Irreducible modules are involved in the definition of a number of important classes of rings: classical semi-simple rings, primitive rings, and others (cf. Classical semi-simple ring; Primitive ring).
References
| [1] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
| [2] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) |
| [3] | J. Lambek, "Lectures on rings and modules" , Blaisdell (1966) |
| [4] | C. Faith, "Algebra: rings, modules, and categories" , 1–2 , Springer (1973–1976) |
Irreducible module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Irreducible_module&oldid=42959