Aleksandrov compactification
Aleksandrov compact extension
The unique Hausdorff compactification 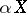 of a locally compact, non-compact, Hausdorff space
of a locally compact, non-compact, Hausdorff space 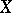 , obtained by adding a single point
, obtained by adding a single point 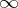 to
to 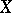 . An arbitrary neighbourhood of the point
. An arbitrary neighbourhood of the point  must then have the form
must then have the form  , where
, where  is some compactum in
is some compactum in  . The Aleksandrov compactification
. The Aleksandrov compactification 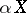 is the smallest element in the set
is the smallest element in the set 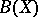 of all compactifications of
of all compactifications of 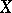 . A smallest element in the set
. A smallest element in the set 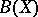 exists only for a locally compact space
exists only for a locally compact space 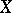 and must coincide with
and must coincide with 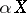 .
.
The Aleksandrov compactification was defined by P.S. Aleksandrov [1] and plays an important role in topology. Thus, the Aleksandrov compactification 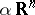 of the
of the  -dimensional Euclidean space is identical with the
-dimensional Euclidean space is identical with the  -dimensional sphere; the Aleksandrov compactification
-dimensional sphere; the Aleksandrov compactification 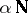 of the set of natural numbers is homeomorphic to the space of a convergent sequence together with the limit point; the Aleksandrov compactification of the "open" Möbius strip coincides with the real projective plane
of the set of natural numbers is homeomorphic to the space of a convergent sequence together with the limit point; the Aleksandrov compactification of the "open" Möbius strip coincides with the real projective plane  . There are pathological situations connected with the Aleksandrov compactification, e.g. there exists a perfectly-normal, locally compact and countably-compact space
. There are pathological situations connected with the Aleksandrov compactification, e.g. there exists a perfectly-normal, locally compact and countably-compact space 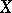 whose Aleksandrov compactification has the dimensions
whose Aleksandrov compactification has the dimensions 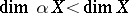 and
and 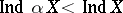 .
.
References
| [1] | P.S. [P.S. Aleksandrov] Aleksandroff, "Ueber die Metrisation der im Kleinen kompakten topologischen Räumen" Math. Ann. , 92 (1924) pp. 294–301 |
Comments
The Aleksandrov compactification is also called the one-point compactification.
References
| [a1] | J. Dugundji, "Topology" , Allyn & Bacon (1966) (Theorem 8.4) |
Aleksandrov compactification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Aleksandrov_compactification&oldid=42709