Cartesian-closed category
A category  such that the following axioms are satisfied:
such that the following axioms are satisfied:
A1) there exists a terminal object  ;
;
A2) for any pair  ,
,  of objects of
of objects of  there exist a product
there exist a product  and given projections
and given projections  ,
,  ;
;
A3) for any pair  ,
,  of objects of
of objects of  there exist an object
there exist an object 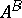 and an evaluation arrow
and an evaluation arrow  such that for any arrow
such that for any arrow  there is a unique arrow
there is a unique arrow 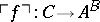 with
with  .
.
These conditions are equivalent to the following:  is a category with given products such that the functors
is a category with given products such that the functors
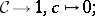 |
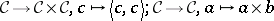 |
have each a specified right-adjoint, written respectively as:
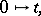 |
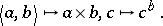 |
Some examples of Cartesian-closed categories are:
E1) any Heyting algebra  ;
;
E2) the category 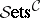 for any small category
for any small category  with
with 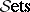 the category of (small) sets — in particular
the category of (small) sets — in particular  itself;
itself;
E3) the category of sheaves over a topological space, and more generally a (Grothendieck) topos;
E4) any elementary topos  ;
;
E5) the category  of all (small) categories;
of all (small) categories;
E6) the category  of graphs and their homomorphisms;
of graphs and their homomorphisms;
E7) the category  -
- of
of  -CPOs.
-CPOs.
These definitions can all be put into a purely equational form.
References
| [a1] | M. Barr, C. Wells, "Category theory for computing science" , CRM (1990) |
| [a2] | J. Lambek, P.J. Scott, "Introduction to higher order categorical logic" , Cambridge Univ. Press (1986) |
| [a3] | S. MacLane, I. Moerdijk, "Sheaves in geometry and logic" , Springer (1992) |
| [a4] | S. MacLane, "Categories for the working mathematician" , Springer (1971) |
Cartesian-closed category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cartesian-closed_category&oldid=42620