Semi-simple matrix
A square matrix over a field 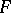 similar to a matrix of the form
similar to a matrix of the form  , where
, where  is a matrix over
is a matrix over  whose characteristic polynomial is irreducible in
whose characteristic polynomial is irreducible in 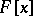 ,
, 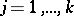 (cf. Irreducible polynomial). For a matrix
(cf. Irreducible polynomial). For a matrix  over a field
over a field  , the following three statements are equivalent: 1)
, the following three statements are equivalent: 1)  is semi-simple; 2) the minimum polynomial of
is semi-simple; 2) the minimum polynomial of 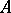 has no multiple factors in
has no multiple factors in 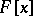 ; and 3) the algebra
; and 3) the algebra 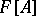 is semi-simple (cf. Semi-simple algebra).
is semi-simple (cf. Semi-simple algebra).
If 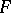 is a perfect field, then a semi-simple matrix over
is a perfect field, then a semi-simple matrix over 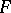 is similar to a diagonal matrix over a certain extension of
is similar to a diagonal matrix over a certain extension of 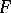 . For any square matrix
. For any square matrix 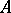 over a perfect field there is a unique representation in the form
over a perfect field there is a unique representation in the form 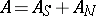 , where
, where 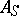 is a semi-simple matrix,
is a semi-simple matrix, 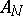 is nilpotent and
is nilpotent and  ; the matrices
; the matrices 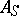 and
and 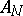 belong to the algebra
belong to the algebra 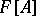 .
.
References
| [1] | N. Bourbaki, "Algèbre" , Eléments de mathématiques , 2 , Hermann (1959) |
Semi-simple matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-simple_matrix&oldid=42278