Open book decomposition

Let 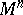be an -dimensional manifold. An open book decomposition of 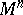consists of a codimension-two submanifold 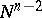, called the binding, and a fibration 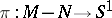. The fibres are called the pages. One may require the fibration to be well behaved near 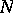, i.e. that 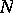have a tubular neighbourhood 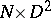such that 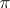restricted to 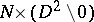is the mapping .

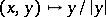The existence of an open book decomposition for any closed, orientable -manifold was proved by J.W. Alexander [a1]. He suggested that the binding may be assumed connected, but the first published proof of this fact was given by R. Myers [a4]. An independent proof (unpublished) is due to F.J. González-Acuña, see also [a5]. Any closed manifold of odd dimension 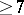admits an open book decomposition [a3], and the same is true for any simply-connected manifold of even dimension 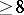with vanishing index [a7].

Such structure theorems have been used to give explicit geometric constructions of contact structures and codimension-one foliations; see, for instance, [a6], [a2].

References

[a1]	J.W. Alexander, "A lemma on systems of knotted curves" Proc. Nat. Acad. Sci. USA , 9 (1923) pp. 93–95 Zbl 49.0408.03
[a2]	A.H. Durfee, H.B. Lawson Jr., "Fibered knots and foliations of highly connected manifolds" Invent. Math. , 17 (1972) pp. 203–215 MR0326752 Zbl 0231.57015
[a3]	T. Lawson, "Open book decompositions for odd dimensional manifolds" Topology , 17 (1978) pp. 189–192 MR0494132 Zbl 0384.57007
[a4]	R. Myers, "Open book decompositions of -manifolds" Proc. Amer. Math. Soc. , 72 (1978) pp. 397–402
[a5]	D. Rolfsen, "Knots and links" , Publish or Perish (1976) MR0515288 Zbl 0339.55004
[a6]	W.P. Thurston, H.E. Winkelnkemper, "On the existence of contact forms" Proc. Amer. Math. Soc. , 52 (1975) pp. 345–347 MR0375366 Zbl 0312.53028
[a7]	H.E. Winkelnkemper, "Manifolds as open books" Bull. Amer. Math. Soc. , 79 (1973) pp. 45–51 MR0310912 Zbl 0269.57011