Lambert transform
From Encyclopedia of Mathematics
The integral transform
 |
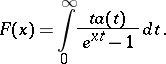The Lambert transform is the continuous analogue of the Lambert series (under the correspondence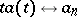 
, 
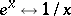). The following inversion formula holds: Suppose that
 |
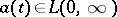and that
 |
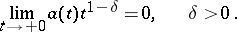If also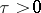 
and if the function 
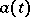is continuous at 
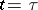, then one has
 |
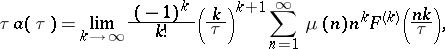where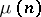 
is the Möbius function.
References
| [1] | D.V. Widder, "An inversion of the Lambert transform" Math. Mag. , 23 (1950) pp. 171–182 |
| [2] | V.A. Ditkin, A.P. Prudnikov, "Integral transforms" Progress in Math. , 4 (1969) pp. 1–85 Itogi Nauk. Mat. Anal. 1966 (1967) pp. 7–82 |
How to Cite This Entry:
Lambert transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lambert_transform&oldid=42007
Lambert transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lambert_transform&oldid=42007
This article was adapted from an original article by Yu.A. BrychkovA.P. Prudnikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article