Retract

of an object of a category

A concept generalizing the corresponding concepts in algebra and topology. An object 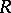of a category 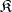is called a retract of an object 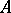if there exist morphisms

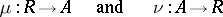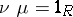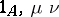such that . The morphism in this case is a monomorphism and, moreover, the equalizer of the pair of morphisms . Dually, the morphism is an epimorphism and also the co-equalizer of the pair of morphisms 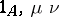. 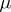is sometimes known as a section and as a retraction.

If 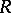is a retract of an object 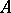and an object 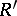is isomorphic to 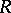, then 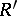is a retract of 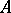. Therefore an isomorphism class of retracts forms a single subobject of 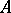. Each retract of 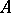, defined by morphisms 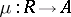and 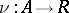, corresponds to an idempotent morphism 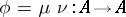. Two retracts 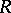and 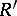of an object 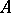belong to the same subobject if and only if they correspond to the same idempotent. The retracts of any object of an arbitrary category form a set.

Comments

The last sentence above is true only if one assumes that all categories involved are locally small (i.e. "have small hom-sets" ) (cf. also Small category).