Artin-Schreier theory
The phrase "Artin–Schreier theory" usually refers to a chapter in the theory of ordered fields.
A formally real field 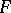 has the property that the only solutions of
has the property that the only solutions of 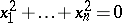 are
are 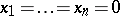 . Any such field can be ordered and, conversely, any ordered field is formally real. A real-closed field is a formally real field that is maximal under algebraic extensions. If
. Any such field can be ordered and, conversely, any ordered field is formally real. A real-closed field is a formally real field that is maximal under algebraic extensions. If 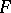 is real closed, then
is real closed, then 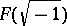 is algebraically closed and, conversely, if
is algebraically closed and, conversely, if 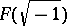 is algebraically closed and
is algebraically closed and 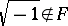 , then
, then 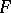 is real closed (the Artin–Schreier characterization of real-closed fields). A further Artin–Schreier theorem is that if
is real closed (the Artin–Schreier characterization of real-closed fields). A further Artin–Schreier theorem is that if 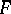 is the algebraic closure of
is the algebraic closure of 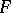 ,
, 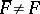 and
and 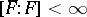 , then
, then 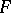 is real closed and hence of characteristic zero and
is real closed and hence of characteristic zero and 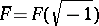 .
.
The theory of formally real fields led E. Artin to the solution of the Hilbert problem on the resolution of definite rational functions as sums of squares (the Artin theorem): Let 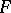 be a field of real numbers, i.e. a subfield of the field of real numbers
be a field of real numbers, i.e. a subfield of the field of real numbers 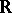 , which has a unique ordering, and let
, which has a unique ordering, and let 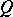 be a rational function (of several variables) with coefficients in
be a rational function (of several variables) with coefficients in 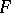 that is rationally definite in the sense that
that is rationally definite in the sense that 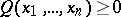 for all
for all  for which
for which 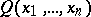 is defined. Then
is defined. Then 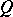 is a sum of squares of rational functions with coefficients in
is a sum of squares of rational functions with coefficients in 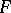 .
.
References
| [a1] | N. Jacobson, "Lectures in abstract algebra" , III: theory of fields and Galois theory , v. Nostrand (1964) pp. Chapt. VI |
| [a2] | P. Ribenboim, "L'arithmétique des corps" , Hermann (1972) pp. Chapt. IX |
Artin-Schreier theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Artin-Schreier_theory&oldid=41904