Baer group
A Baer subplane in a projective plane is a subplane with the property that any point of the plane is incident with a line of the subplane and any line of the plane intersects the subplane in at least one point. For finite projective planes, the order of the plane is  when there are exactly
when there are exactly 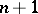 points per line. A subplane of order
points per line. A subplane of order 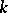 in a projective plane
in a projective plane  is Baer if and only if
is Baer if and only if 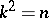 . A Baer group is a collineation group of a projective plane which fixes each point of a Baer subplane. It is possible to use Baer groups to characterize those planes which correspond to hyperbolic and conical flocks (cf. also Flock). If the flock is in
. A Baer group is a collineation group of a projective plane which fixes each point of a Baer subplane. It is possible to use Baer groups to characterize those planes which correspond to hyperbolic and conical flocks (cf. also Flock). If the flock is in 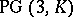 , for
, for 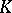 a field, a Baer subplane fixed pointwise by a Baer group is a line of
a field, a Baer subplane fixed pointwise by a Baer group is a line of 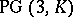 which is not in the spread (cf. Flock). A Baer group is maximal of elation, respectively homology, type if the group acts transitively on the non-fixed points on each line
which is not in the spread (cf. Flock). A Baer group is maximal of elation, respectively homology, type if the group acts transitively on the non-fixed points on each line 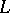 of the spread which intersects the Baer subplane and fixes one, respectively two, point(s) of
of the spread which intersects the Baer subplane and fixes one, respectively two, point(s) of 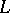 .
.
The translation planes with spread in 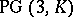 that admit maximal Baer groups of elation or homology type are in one-to-one correspondence with partial conical or hyperbolic flocks of deficiency one, respectively (see Flock (also for additional references); [a1], [a2]).
that admit maximal Baer groups of elation or homology type are in one-to-one correspondence with partial conical or hyperbolic flocks of deficiency one, respectively (see Flock (also for additional references); [a1], [a2]).
References
| [a1] | N.L. Johnson, "Flocks of hyperbolic quadrics and translation planes admitting affine homologies" J. Geom. , 34 (1989) pp. 50–73 |
| [a2] | V. Jha, N.L. Johnson, "Structure theory for point-Baer and line-Baer collineation groups in affine planes" , Proc. Amer. Math. Soc. Conf. Iowa City (l996) |
Baer group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baer_group&oldid=41784