Meier theorem

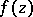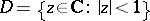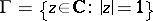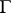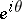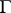Let be a meromorphic function in the unit disc ; then all points of the circle except, possibly, for a set of the first category on , are either Plessner points or Meier points. By definition, a point on is a Plessner point for 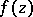if the angular cluster set 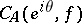is total (i.e., coincides with the whole extended complex plane 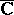) for every angle 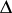between pairs of chords through 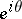. 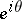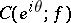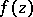The point is said to be a Meier point (or to have the Meier property) if: 1) the complete cluster set of at 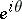is subtotal, i.e. does not coincide with the whole extended complex plane 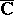; and 2) the set of all limit values along arbitrary chords of the disc 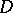drawn at the point 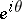is identical to 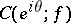. The theorem was proved by K. Meier [1].

Meier's theorem is the analogue, in terms of the category of a set, of the Plessner theorem, which is formulated in terms of measure theory. A sharpening of Meier's theorem is given in [3].

References

[1]	K. Meier, "Ueber die Randwerte der meromorphen Funktionen" Math. Ann , 142 (1961) pp. 328–344
[2]	E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 1;6
[3]	V.I. Gavrilov, A.N. Kanatnikov, "Characterization of the set 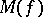for meromorphic functions" Soviet Math. Dokl. , 18 : 2 (1977) pp. 15–17 Dokl. Akad. Nauk SSSR , 233 : 1 (1977)