Dimension function
From Encyclopedia of Mathematics
An integer-valued function 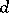 on a lattice
on a lattice  (that is, a mapping
(that is, a mapping 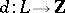 ) that satisfies the conditions: 1)
) that satisfies the conditions: 1) 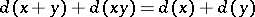 for any
for any 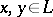 ; and 2) if
; and 2) if 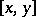 is an elementary interval in
is an elementary interval in 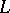 , then
, then 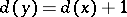 . For a lattice in which all bounded chains are finite, the existence of a dimension function is equivalent to the modular property.
. For a lattice in which all bounded chains are finite, the existence of a dimension function is equivalent to the modular property.
There is also a more general definition of a dimension function on an orthomodular lattice or on an orthomodular partially ordered set, where the values of the dimension function can be arbitrary real numbers, or even functions (see [3]).
References
| [1] | L.A. Skornyakov, "Elements of lattice theory" , Hindushtan Publ. Comp. (1977) (Translated from Russian) |
| [2] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [3] | G. Kalmbach, "Orthomodular lattices" , Acad. Press (1983) |
How to Cite This Entry:
Dimension function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dimension_function&oldid=40056
Dimension function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dimension_function&oldid=40056
This article was adapted from an original article by T.S. Fofanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article