Bloch function
Let  be the open unit disc in
be the open unit disc in  . A holomorphic function
. A holomorphic function  on
on  is called a Bloch function if it has the property that
is called a Bloch function if it has the property that
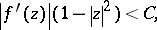 | (a1) |
for a positive constant  , independent of
, independent of  . The Bloch norm of
. The Bloch norm of  is
is  , where
, where  is the infimum of the constants
is the infimum of the constants  for which (a1) holds. The Bloch norm turns the set of Bloch functions into a Banach space,
for which (a1) holds. The Bloch norm turns the set of Bloch functions into a Banach space,  , and
, and  is a Möbius-invariant semi-norm on
is a Möbius-invariant semi-norm on 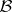 (cf. also Fractional-linear mapping).
(cf. also Fractional-linear mapping).
Bloch functions appear naturally in connection with Bloch's theorem. Call a disc in  in the image of
in the image of 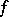 schlicht if it is the univalent image of some open set (cf. Univalent function). Bloch's theorem can be stated as follows. There is a constant
schlicht if it is the univalent image of some open set (cf. Univalent function). Bloch's theorem can be stated as follows. There is a constant 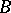 (the Bloch constant) such that the image of every holomorphic function
(the Bloch constant) such that the image of every holomorphic function 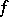 with
with  ,
, 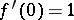 contains the schlicht disc
contains the schlicht disc  .
.
A disc automorphism leads to schlicht discs of radius at least  about
about 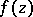 . The radii of the schlicht discs of Bloch functions are therefore bounded.
. The radii of the schlicht discs of Bloch functions are therefore bounded.
The following properties of Bloch functions are well-known.
i) Bounded holomorphic functions, and moreover analytic functions with boundary values in  (cf.
(cf. 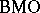 -space), are in
-space), are in  .
.
ii)  coincides with the class of analytic functions that are in
coincides with the class of analytic functions that are in  of the disc.
of the disc.
iii)  is the largest Möbius-invariant space of holomorphic functions on
is the largest Möbius-invariant space of holomorphic functions on  that possesses non-zero continuous functionals that are also continuous with respect to some Möbius-invariant semi-norm, cf. [a3].
that possesses non-zero continuous functionals that are also continuous with respect to some Möbius-invariant semi-norm, cf. [a3].
iv) Bloch functions are normal, i.e., if 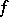 is Bloch, then
is Bloch, then  is a normal family.
is a normal family.
v) Boundary values of Bloch functions need not exist; also, the radial limit function can be bounded almost-everywhere, while the Bloch function is unbounded. (Cf. [a1], [a2].)
The concept of a Bloch function has been extended to analytic functions of several complex variables on a domain  . This can be done by replacing (a1) by the estimates
. This can be done by replacing (a1) by the estimates
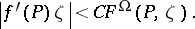 |
Here 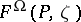 denotes the Kobayashi metric of
denotes the Kobayashi metric of  at
at 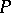 in the direction
in the direction  . (Cf. [a2], [a4], [a5].)
. (Cf. [a2], [a4], [a5].)
References
| [a1] | J.M. Anderson, J. Clunie, Ch. Pommerenke, "On Bloch functions and normal functions" J. Reine Angew. Math. , 270 (1974) pp. 12–37 |
| [a2] | S.G. Krantz, "Geometric analysis and function spaces" , CBMS , 81 , Amer. Math. Soc. (1993) |
| [a3] | L. Rubel, R. Timoney, "An extremal property of the Bloch space" Proc. Amer. Math. Soc. , 43 (1974) pp. 306–310 |
| [a4] | R. Timoney, "Bloch functions in several complex variables, I" Bull. London Math. Soc. , 12 (1980) pp. 241–267 |
| [a5] | R. Timoney, "Bloch functions in several complex variables, II" J. Reine Angew. Math. , 319 (1980) pp. 1–22 |
Bloch function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bloch_function&oldid=39741