Trigonometric interpolation

The approximate representation of a function 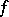in the form of a trigonometric polynomial

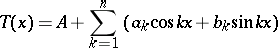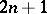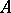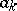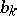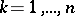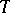whose values coincide at prescribed points with the corresponding values of the function. Thus, it is always possible to choose the coefficients , , , , of the -th order polynomial so that its values are equal to the values 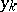of the function at 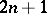preassigned points 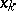in the interval 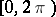. The polynomial has the form

(*)

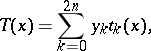where

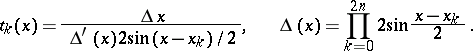The polynomial 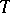assumes an especially simple form in case the nodes 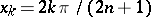are equi-distant; the coefficients are given by the formulas

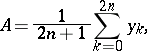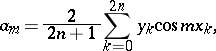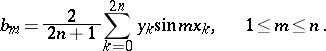Comments

The formula (*) above for the trigonometric polynomial taking the prescribed values 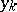at the nodes 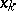is known as the Gauss formula of trigonometric interpolation, [a2].

References

[a1]	A. Zygmund, "Trigonometric series" , 2 , Cambridge Univ. Press (1988)
[a2]	P.J. Davis, "Interpolation and approximation" , Dover, reprint (1975) pp. 29, 38