Hyperbolic paraboloid
A non-closed non-central surface of the second order. In a suitable coordinate system (see Fig.) the equation of a hyperbolic paraboloid is
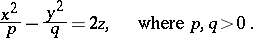 |
Sections of a hyperbolic paraboloid by planes parallel to the planes 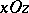 and
and 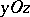 are parabolas, while sections by planes parallel to the plane
are parabolas, while sections by planes parallel to the plane 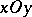 are hyperbolas (the section by the plane
are hyperbolas (the section by the plane 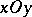 consists of two straight lines). The symmetry axis of a hyperbolic paraboloid is said to be its axis; the point of intersection of a hyperbolic paraboloid with the axis is known as the apex. If
consists of two straight lines). The symmetry axis of a hyperbolic paraboloid is said to be its axis; the point of intersection of a hyperbolic paraboloid with the axis is known as the apex. If  , the hyperbolic paraboloid has two axes of symmetry.
, the hyperbolic paraboloid has two axes of symmetry.
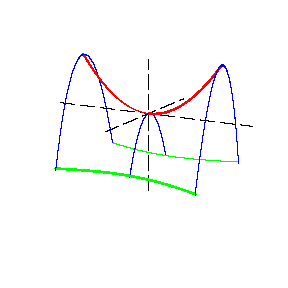
Figure: h048290a
A hyperbolic paraboloid is a ruled surface; the equations of the rectilinear generators passing through a given point 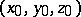 have the form
have the form
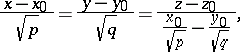 |
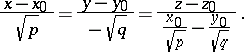 |
Comments
References
| [a1] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [a2] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German) |
Hyperbolic paraboloid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_paraboloid&oldid=38839