Homotopy polynomial

An invariant of oriented links (cf. also Link).

It is a polynomial of two variables associated to homotopy classes of links in , depending only on linking numbers between components ([a1], cf. also Knot theory). It satisfies the skein relation (cf. also Conway skein triple)

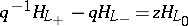for a mixed crossing. The homotopy polynomial of a link with diagram 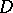is closely related to the dichromatic polynomial of the graph associated to 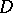(cf. also Graph colouring). The homotopy polynomial can be generalized to homotopy skein modules of three-dimensional manifolds (cf. also Skein module).

References

[a1]	J.H. Przytycki, "Homotopy and 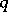-homotopy skein modules of -manifolds: An example in Algebra Situs" , Proc. Conf. in Low-Dimensional Topology in Honor of Joan Birman's 70th Birthday (Columbia Univ./Barnard College, March, 14-15, 1998) , Internat. Press (2000)