Semi-simple endomorphism

semi-simple linear transformation, of a vector space over a field

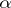An endomorphism of with the following property: For any -invariant subspace of there exists an -invariant subspace such that 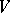is the direct sum of 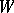and 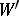. In other words, 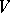should be a semi-simple module over the ring 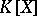, acting as 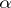. For example, any orthogonal, symmetric or skew-symmetric linear transformation of a finite-dimensional Euclidean space, and also any diagonalizable (i.e. representable by a diagonal matrix with respect to some basis) linear transformation of a finite-dimensional vector space, is a semi-simple endomorphism. The semi-simplicity of an endomorphism is preserved by passage to an invariant subspace 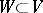, and to the quotient space .

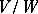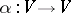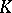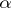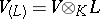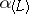Let . An endomorphism is semi-simple if and only if its minimum polynomial (cf. Matrix) has no multiple factors. Let be an extension of the field and let be the extension of the endomorphism to the space . If is semi-simple, then 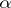is also semi-simple, and if 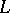is separable over 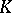, then the converse is true. An endomorphism 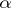is called absolutely semi-simple if 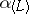is semi-simple for any extension 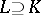; for this it is necessary and sufficient that the minimum polynomial has no multiple roots in the algebraic closure 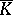of 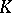, that is, that the endomorphism 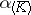is diagonalizable.

References

[1]	N. Bourbaki, "Algèbre" , Eléments de mathématiques , Hermann (1970) pp. Chapts. I-III

Comments

Over an algebraically closed field any endomorphism of a finite-dimensional vector space can be decomposed into a sum of a semi-simple endomorphism and a nilpotent one such that ; cf. Jordan decomposition, 2).