Matrix factorization

factorization of matrices

Factorizations of matrices over a field are useful in quite a number of problems, both analytical and numerical; for example, in the (numerical) solution of linear equations and eigenvalue problems. A few well-known factorizations are listed below.

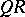-factorization.

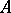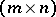Let be an -matrix with 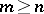over 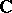. Then there exist a unitary 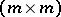-matrix 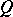and a right-triangular 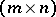-matrix 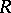such that 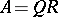. Here, a right-triangular 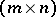-matrix, 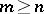, is of the form

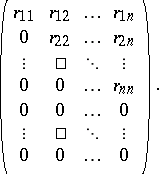A real (respectively, complex) non-singular matrix 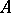has a factorization 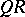with 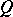orthogonal (respectively, unitary) and 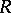having all elements positive. Such a factorization is unique and given by the Gram–Schmidt orthogonalization process (cf. Orthogonalization method). The frequently used 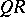-algorithm for eigenvalue problems (cf. Iteration methods) is based on repeated 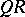-factorization.

Singular value factorization.

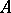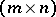Let be an -matrix over 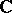of rank 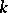. Then it can be written as 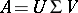, with 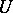a unitary 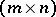-matrix, 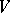a unitary 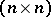-matrix and 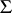of the form

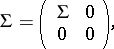where is diagonal with as entries the singular values of 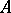, i.e. the positive square roots of the eigenvalues of 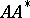(equivalently, of ).

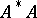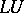-factorization.

An 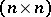-matrix 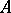(over a field) such that the leading principal minors are non-zero,

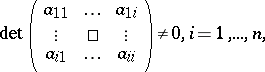can be written as a product 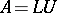with 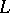a lower-triangular matrix and 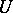an upper-triangular matrix. This is also known as triangular factorization. This factorization is unique if the diagonal elements of 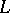(respectively, 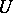) are specified (e.g., all equal to 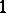); see, e.g., [a2], p. 821. Conversely, if 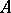is invertible and 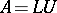, then all leading principal minors are non-zero.

In general, permutations of rows (or columns) are needed to obtain a triangular factorization. For any 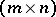-matrix there are a permutation matrix 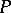, a lower-triangular matrix 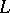with unit diagonal and an 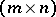echelon matrix 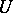such that 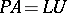. Here, an echelon matrix can be described as follows:

i) the non-zero rows come first (the first non-zero entry in a row is sometimes called a pivot);

ii) below each pivot is a column of zeros;

iii) each pivot lies to the right of the pivot in the row above. For example,

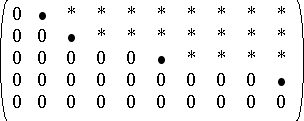where the pivots are denoted by . 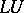-factorization is tightly connected with Gaussian elimination, see Gauss method and [a3].

Iwasawa decomposition.

The 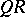-factorization for real non-singular matrices immediately leads to the Iwasawa factorization 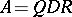with 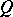orthogonal, 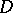diagonal and 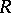an upper (or lower) triangular matrix with 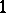s on the diagonal, giving an Iwasawa decomposition for any non-compact real semi-simple Lie group.

Choleski factorization.

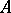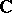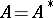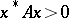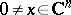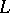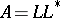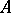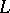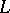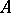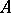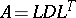For each Hermitean positive-definite matrix over (i.e., , for all ) there is a unique lower-triangular matrix with positive diagonal entries such that . If is real, so is . See, e.g., [a4], p. 180ff. This is called a Choleski factor. An incomplete Choleski factorization of a real positive-definite symmetric is a factorization of as with 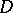a positive-definite diagonal matrix and 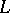lower-triangular.

Decomposition of matrices.

Instead of "factorization" , the word "decomposition" is also used: Choleski decomposition, 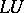-decomposition, 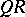-decomposition, triangular decomposition.

However, decomposition of matrices can also mean, e.g., block decomposition in block-triangular form:

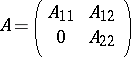and a decomposable matrix is generally understood to mean a matrix that, via a similarity transformation, can be brought to the form

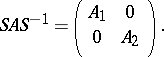Still other notions of decomposable matrix exist, cf., e.g., [a10].

Matrices over function fields.

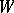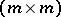For matrices over function fields there are (in addition) other types of factorizations that are important. E.g., let be an -matrix with coefficients in the field of rational functions 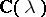and without poles in 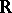or at 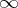. Assume also that for 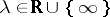. Then there are rational function matrices 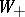and 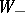, also without poles in 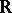or at 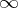, and integers 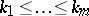such that

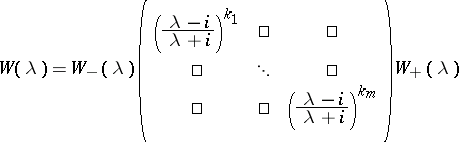and

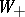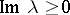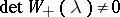a) has no poles in and for ;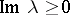

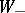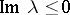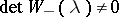b) has no poles in and for ;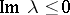

c) 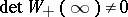; 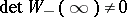. This is called a Wiener–Hopf factorization; more precisely, a right Wiener–Hopf factorization with respect to the real line. There are also left Wiener–Hopf factorizations (with 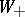and 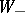interchanged) and Wiener–Hopf factorizations with respect to the circle (or any other contour in ).

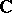In the scalar case, 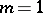, the factors 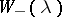and 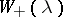are unique. This is no longer the case for 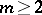(however, the indices 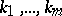are still unique). See also Integral equation of convolution type.

If all indices in the decomposition are zero, one speaks of a right canonical factorization. For more, and also about spectral factorization and minimal factorization, and applications, see [a5], [a6], [a7].

Matrix polynomials.

The factorization of matrix polynomials, i.e., the study of the division structure of the ring of 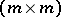-matrices with polynomial entries, is a quite different matter. See [a8], [a9] for results in this direction.

References

[a1]	B. Noble, J.W. Daniel, "Applied linear algebra" , Prentice-Hall (1969) pp. Sect. 9.4–9.5
[a2]	D.M. Young, R.T. Gregory, "A survey of numerical mathematics" , II , Dover (1988)
[a3]	G. Strang, "Linear algebra and its applications" , Harcourt–Brace–Jovanovich (1976)
[a4]	J. Stoer, R. Bulirsch, "Introduction to numerical analysis" , Springer (1993)
[a5]	H. Bart, I. Gohberg, M.A. Kaashoek, "Minimal factorization of matrix and operator functions" , Birkhäuser (1979)
[a6]	K. Clancey, I. Gohberg, "Factorization of matrix functions and singular integral operators" , Birkhäuser (1981)
[a7]	I. Gohberg, S. Goldberg, M.A. Kaashoek, "Classes of linear operators" , I–II , Birkhäuser (1990–1993)
[a8]	A.N. Malyshev, "Matrix equations: Factorization of matrix polynomials" M. Hazewinkel (ed.) , Handbook of Algebra , I , Elsevier (1995) pp. 79–116
[a9]	L. Rodman, "Matrix functions" M. Hazewinkel (ed.) , Handbook of Algebra , I , Elsevier (1995) pp. 117–154
[a10]	M. Marcus, H. Minc, "A survey of matrix theory and matrix inequalities" , Dover (1992) pp. 122ff