Knaster continuum

hereditarily indecomposable continuum

A continuum each subcontinuum of which is indecomposable. A space 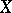is called indecomposable if it is connected and cannot be represented as the union of two closed connected proper subsets of it.

The first proof of the existence of such a continuum was given by B. Knaster [1]. In the space of all subcontinua of the ordinary square 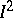, the set of all Knaster continua is an everywhere-dense 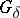-set [2].

References

[1]	B. Knaster, "Un continu dont tout sous-continu est indécomposable" Fund. Math. , 3 (1922) pp. 247–286
[2]	S. Mazurkiewicz, "Sur les continus absolument indécomposables" Fund. Math. , 16 (1930) pp. 151–159

Comments

See also Pseudo-arc and Hereditarily indecomposable continuum.