Balanced set

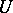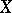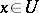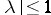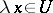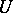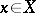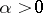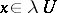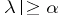A set in a real or complex vector space such that and imply . An example of a balanced set is given by the unit ball in a normed vector space and, generally, by a neighbourhood of zero in a base of neighbourhoods of zero in a topological vector space. These neighbourhoods of zero are moreover absorbing, i.e. such that for any there exists an such that for . If 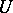is a convex, absorbing and balanced set, then the functional 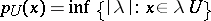is a semi-norm, i.e. it has the properties

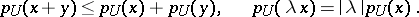A balanced set is also called centred.

References

[1]	L.V. Kantorovich, G.P. Akilov, "Functional analysis" , Pergamon (1982) (Translated from Russian)

Comments

The functional 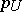mentioned above is also called the Minkowski functional of the convex, absorbing and balanced set .

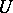References

[a1]	K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5