Trace
From Encyclopedia of Mathematics
The mapping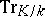 
of a field 
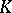into a field 
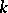(where 
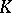is a finite extension of 
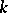) that sends an element 
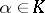to the trace of the matrix (cf. Trace of a square matrix) of the 
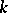-linear mapping 
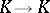sending 
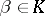to 
. 
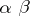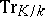is a homomorphism of the additive groups.
If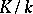 
is a separable extension, then
 |
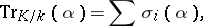where the sum is taken over all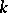 
-isomorphisms 
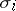of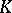 
into an algebraic closure 
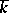of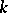 
. The trace mapping is transitive, that is, if 
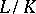and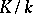 
are finite extensions, then for any 
,
 |
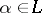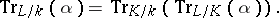Comments
Especially in older mathematical literature, instead of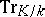 
one finds 
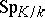(from the German "Spur" ) as notation for this mapping.
References
| [a1] | N. Jacobson, "Lectures in abstract algebra" , 3. Theory of fields and Galois theory , Springer, reprint (1975) |
| [a2] | N. Jacobson, "Basic algebra" , 1 , Freeman (1985) |
| [a3] | S. Lang, "Algebra" , Addison-Wesley (1965) |
How to Cite This Entry:
Trace. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trace&oldid=35824
Trace. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trace&oldid=35824
This article was adapted from an original article by L.V. Kuz'min (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article