Interval order

interval ordering, interval partially ordered set, interval poset

Let 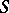be a set of closed intervals of the real line 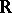. A partial ordering is defined on 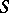by

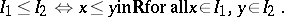Such a partially ordered set (more precisely, one isomorphic to it) is called an interval order.

A linear order, also called a totally ordered set, is an interval order (but an interval order need not be total, of course).

There is the following forbidden sub-poset characterization of interval orders (the Fishburn theorem, [a1]): A poset 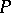is an interval order if and only if 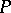does not contain the disjoint sum as a sub-poset (cf. also Disjoint sum of partially ordered sets). Here, 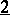is the totally ordered set 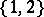, , 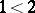so that with 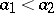, 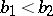and no other comparable pairs of unequal elements.

A poset is called a semi-order if there is a function 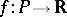such that in 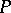if and only if 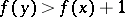. Clearly, a semi-order is isomorphic to an interval order with all intervals of length 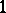. Here too, a forbidden sub-poset characterization holds (the Scott–Suppes theorem, [a2]): A poset 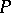is a semi-order if and only if it does not contain eithe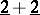r or as a sub-poset.

References

[a1]	P.C. Fishburn, "Intransitive indifference with unequal indifference intervals" J. Math. Psychol. , 7 (1970) pp. 144–149
[a2]	D. Scott, P. Suppes, "Foundational aspects of the theories of measurement" J. Symbolic Logic , 23 (1958) pp. 113–128
[a3]	W.T. Trotter, "Partially ordered sets" R.L. Graham (ed.) M. Grötschel (ed.) L. Lovász (ed.) , Handbook of Combinatorics , I , North-Holland (1995) pp. 433–480