Relatively-open (-closed) set
From Encyclopedia of Mathematics
set open (closed) relative (or with respect to) to a certain set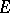 
in a topological space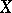 
A set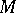 
in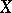 
such that
 |
(the bar denotes the operation of closure, cf. Closure of a set). For a certain set to be open (closed) relative to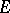 
, it is necessary and sufficient that it is the intersection of 
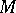and a certain open (closed) set.
Comments
A set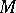 
in a topological space is relatively open (relatively closed) with respect to 
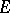if and only if 
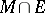is open (respectively, closed) in 
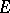for the relative topology on 
.
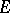References
| [a1] | P.S. [P.S. Aleksandrov] Alexandroff, H. Hopf, "Topologie" , Chelsea, reprint (1972) pp. 33ff, 44ff |
| [a2] | C. Kuratowski, "Introduction to set theory and topology" , Pergamon (1961) pp. 128ff (Translated from French) |
How to Cite This Entry:
Relatively-open (-closed) set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Relatively-open_(-closed)_set&oldid=34421
Relatively-open (-closed) set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Relatively-open_(-closed)_set&oldid=34421
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article