Heinz inequality
In the sequel, a capital letter denotes a bounded linear operator on a Hilbert space 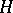 . An operator
. An operator 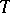 is said to be positive (denoted by
is said to be positive (denoted by 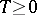 ) if
) if 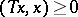 for all
for all 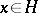 . In 1951, E. Heinz [a3] proved a series of very useful norm inequalities; one of the most essential inequalities in operator theory being:
. In 1951, E. Heinz [a3] proved a series of very useful norm inequalities; one of the most essential inequalities in operator theory being:
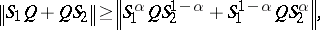 | (a1) |
where 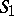 and
and 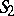 are positive operators and
are positive operators and 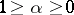 .
.
It is shown in [a1] and [a2] that the Heinz inequality (a1) is equivalent to each of the inequalities (a2), (a3) and (a4). Other norm inequalities equivalent to (a1) have also been obtained in [a1] and [a2]. For any operators 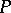 ,
, 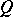 and
and 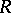 ,
,
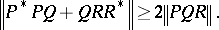 | (a2) |
For a self-adjoint and invertible operator 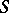 ,
,
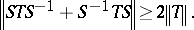 | (a3) |
For 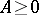 and self-adjoint
and self-adjoint 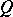 ,
,
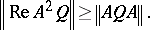 | (a4) |
The inequality (a2) has been obtained in [a4] to give an alternative ingenious proof of (a1). The original proof of the Heinz inequality (a1), based on deep calculations in complex analysis, is shown in [a3]; a simplified and elementary proof of (a1) is given in [a2].
See also Heinz–Kato inequality; Heinz–Kato–Furuta inequality.
References
| [a1] | J.I. Fujii, M. Fujii, T. Furuta, R. Nakamoto, "Norm inequalities related to McIntosh type inequality" Nihonkai Math. J. , 3 (1992) pp. 67–72 |
| [a2] | J.I. Fujii, M. Fujii, T. Furuta, R. Nakamoto, "Norm inequalities equivalent to Heinz inequality" Proc. Amer. Math. Soc. , 118 (1993) pp. 827–830 |
| [a3] | E. Heinz, "Beiträge zur Störungstheorie der Spektralzerlegung" Math. Ann. , 123 (1951) pp. 415–438 |
| [a4] | A. McIntosh, "Heinz inequalities and perturbation of spectral families" Macquarie Math. Reports (1979) pp. unpublished |
Heinz inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Heinz_inequality&oldid=34401