Hewitt realcompactification
Hewitt compactification, Hewitt extension
An extension of a topological space that is maximal relative to the property of extending real-valued continuous functions; it was proposed by E. Hewitt in [1].
A homeomorphic imbedding  is called a functional extension if
is called a functional extension if 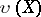 is dense in
is dense in 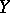 and if for every continuous function
and if for every continuous function 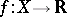 there exists a continuous function
there exists a continuous function  such that
such that 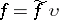 . A completely-regular space
. A completely-regular space 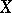 is called a
is called a 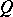 -space or a functionally-complete space if every functional extension of it is a homeomorphism, that is, if
-space or a functionally-complete space if every functional extension of it is a homeomorphism, that is, if 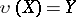 . A functional extension
. A functional extension 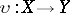 of a completely-regular space is called a Hewitt extension if
of a completely-regular space is called a Hewitt extension if 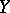 is a
is a 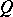 -space. A completely-regular space has a Hewitt extension, and the latter is unique up to a homeomorphism.
-space. A completely-regular space has a Hewitt extension, and the latter is unique up to a homeomorphism.
The Hewitt extension can also be defined as the subspace of those points 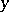 of the Stone–Čech compactification
of the Stone–Čech compactification 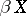 for which every continuous real-valued function
for which every continuous real-valued function 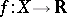 can be extended to
can be extended to 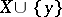 .
.
References
| [1] | E. Hewitt, "Rings of real-valued continuous functions, I" Trans. Amer. Math. Soc. , 64 (1948) pp. 45–99 |
| [2] | R. Engelking, "Outline of general topology" , North-Holland (1968) (Translated from Polish) |
| [3] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
Comments
The Hewitt extension is not a compactification, hence the phrase "Hewitt compactification" is rarely used.
Hewitt realcompactification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hewitt_realcompactification&oldid=34335