Oscillating matrix

oscillatory matrix

A totally non-negative matrix 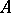for which there exists a positive integer 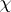such that 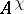is a totally positive matrix; the matrix 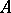is called totally non-negative (totally positive) if all its minors, of whatever order, are non-negative (positive). The lowest exponent 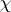is called the exponent of the oscillating matrix. If 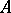is an oscillating matrix with exponent 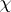, then for any integer 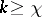the matrix 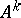is totally positive; an integer positive power of an oscillating matrix and the matrix 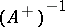are also oscillating matrices. In order that a totally non-negative matrix 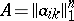is an oscillating matrix, it is necessary and sufficient that: 1) 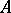is a non-singular matrix; and 2) for 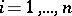, the following are fulfilled: , .

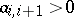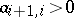The basic theorem on oscillating matrices is: An oscillating matrix 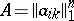always has different positive eigen values; for the eigen vector that corresponds to the largest eigen value 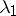, all coordinates differ from zero and are of the same sign; for an eigen vector that corresponds to the -th eigen value (arranged according to decreasing value) there are exactly 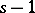changes of sign; for any real numbers , , 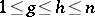, 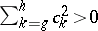the number of changes of sign in the sequence of coordinates of the vector is between and .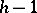

References

[1]	F.R. Gantmakher, M.G. Krein, "Oscillation matrices and kernels and small vibrations of mechanical systems" , Dept. Commerce USA. Joint Publ. Service (1961) (Translated from Russian)

References

[a1]	S. Karlin, "Total positivity" , Stanford Univ. Press (1960)
[a2]	F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 2 , Chelsea, reprint (1959) pp. Chapt. XIII, §9 (Translated from Russian)