Gauss-Lucas theorem
From Encyclopedia of Mathematics
Revision as of 18:52, 24 March 2012 by Ulf Rehmann (talk | contribs) (moved Gauss–Lucas theorem to Gauss-Lucas theorem: ascii title)
Gauss theorem
Let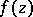 
be a complex polynomial, i.e., 
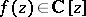. Then the zeros of the derivative 
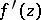are inside the convex polygon spanned by the zeros of 
.
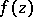References
| [a1] | E. Hille, "Analytic function theory" , 1 , Chelsea, reprint (1982) pp. 84 |
| [a2] | P. Henrici, "Applied and computational complex analysis" , I , Wiley, reprint (1988) pp. 463ff |
| [a3] | B.J. Lewin, "Nullstellenverteilung ganzer Funktionen" , Akademie Verlag (1962) pp. 355 |
How to Cite This Entry:
Gauss-Lucas theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss-Lucas_theorem&oldid=34109
Gauss-Lucas theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss-Lucas_theorem&oldid=34109
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article