Support of a module
From Encyclopedia of Mathematics
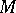over a commutative ring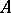 
The set of all prime ideals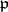 
of 
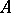for which the localizations 
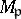of the module are non-zero (cf. Localization in a commutative algebra). This set is denoted by 
. It is a subset of the spectrum of the ring (cf. Spectrum of a ring). For example, for a finite Abelian group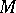 
regarded as a module over the ring of integers, 
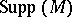consists of all prime ideals 
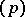, where 
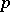divides the order of 
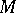. For an arbitrary module 
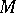the set 
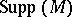is empty if and only if 
.
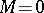References
| [1] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
How to Cite This Entry:
Support of a module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Support_of_a_module&oldid=33862
Support of a module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Support_of_a_module&oldid=33862
This article was adapted from an original article by L.V. Kuz'min (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article