Weyl almost-periodic functions
From Encyclopedia of Mathematics
The class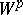 
of complex-valued functions 
, 
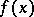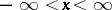, summable to degree 
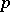on each bounded interval of the real axis and such that for every 
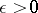there is an 
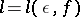for which 
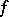has a relatively-dense set 
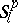of 
-almost-periods (cf. Almost-period). The class was defined by H. Weyl [1]. The class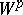 
of Weyl almost-periodic functions is an extension of the class of Stepanov almost-periodic functions.
Weyl almost-periodic functions are related to the metric
 |
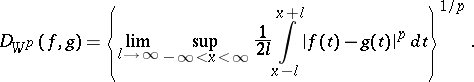If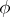 
is a null function in the metric 
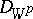, i.e.
 |
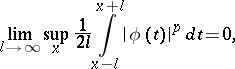and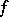 
is a Stepanov almost-periodic function, then
 | (*) |
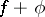is a Weyl almost-periodic function. There also exist Weyl almost-periodic functions which cannot be represented in the form (*); cf. [3].
References
| [1] | H. Weyl, "Integralgleichungen und fastperiodische Funktionen" Math. Ann. , 97 (1927) pp. 338–356 |
| [2] | B.M. Levitan, "Almost-periodic functions" , Moscow (1953) (In Russian) |
| [3] | B.M. Levitan, V.V. Stepanov, "Sur les fonctions presque périodiques apportenant au sens strict à la classe 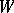 " Dokl. Akad. Nauk SSSR , 22 : 5 (1939) pp. 220–223 |
How to Cite This Entry:
Weyl almost-periodic functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl_almost-periodic_functions&oldid=33675
Weyl almost-periodic functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl_almost-periodic_functions&oldid=33675
This article was adapted from an original article by E.A. Bredikhina (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article