Bezout ring

An integral domain with a unit element in which any ideal of finite type is principal. Any principal ideal ring and also any valuation ring is Bezout. A Bezout ring is integrally closed, and its localizations (i.e. its rings of fractions with respect to multiplicative systems 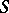, cf. Localization in a commutative algebra) are again Bezout rings. For a finite set of elements of a Bezout ring there exist the greatest common divisor (the greatest common divisor of has the form , , 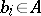a so-called Bezout identity) and the lowest common multiple. A Noetherian ring (and even a ring that satisfies the ascending chain condition only for principal ideals) which is Bezout is a principal ideal ring. As for principal ideal rings, a module of finite type over a Bezout ring is a direct sum of a torsion module and a free module.

References

[a1]	R. Gilmer, "Multiplicative ideal theory" , M. Dekker (1972)