Chiral anomaly

One of the quantum-field theoretic manifestations of chiral dissymmetry or chiral asymmetry. Chiral anomaly in -dimensional quantum field theory means that the quantum field observables from the left and the right sectors of a field model do not commute. Chiral anomaly is deeply related to non-commutative geometry and the theory of anti-commutative algebras (cf. Anti-commutative algebra), which are not Lie algebras [a1], [a2]. 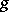Namely, if the chiral sectors admit symmetries described by a semi-simple Lie algebra , then the whole model possesses symmetries, whose generators belong to the Borel–Lie anti-commutative central extension of the double (an anti-commutative algebra is called a Borel–Lie algebra (or BL-algebra) if every solvable subalgebra of it is a Lie algebra).

Field models with chiral anomaly are efficiently used for anomalous stereo-synthesis (e.g., octonionic stereo-synthesis) in real-time interactive binocular video-systems.

References

[a1]	D. Juriev, "Noncommutative geometry, chiral anomaly in the quantum projective -invariant field theory and 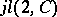-invariance" J. Math. Phys. , 33 (1992) pp. 2819–2822
[a2]	D. Juriev, "Erratum" J. Math. Phys. , 34 (1993) pp. 1615