Rectangle rule
A formula for calculating an integral over a finite interval 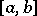 :
:
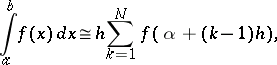 | (*) |
where 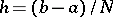 and
and 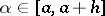 . Its algebraic degree of accuracy is 1 if
. Its algebraic degree of accuracy is 1 if  and 0 otherwise.
and 0 otherwise.
The quadrature formula (*) is exact for the trigonometric functions
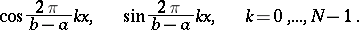 |
If 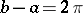 , then (*) is exact for all trigonometric polynomials of order at most
, then (*) is exact for all trigonometric polynomials of order at most 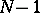 ; moreover, its trigonometric degree of accuracy is
; moreover, its trigonometric degree of accuracy is 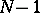 . No other quadrature formula with
. No other quadrature formula with  real nodes can have trigonometric degree of accuracy larger than
real nodes can have trigonometric degree of accuracy larger than 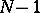 , so that the rectangle rule with
, so that the rectangle rule with 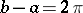 has the highest trigonometric degree of accuracy.
has the highest trigonometric degree of accuracy.
Let 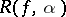 be the error of the rectangle rule, i.e. the difference between the left- and right-hand sides of (*). If the integrand
be the error of the rectangle rule, i.e. the difference between the left- and right-hand sides of (*). If the integrand  is twice continuously differentiable on
is twice continuously differentiable on 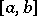 , then for
, then for 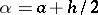 one has
one has
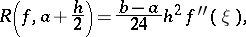 |
for some 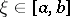 . If
. If 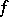 is a periodic function with period
is a periodic function with period 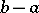 and has a continuous derivative of order
and has a continuous derivative of order 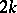 (where
(where  is a natural number) on the entire real axis, then for any
is a natural number) on the entire real axis, then for any 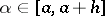 ,
,
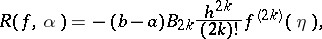 |
for some 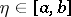 , where
, where  is the Bernoulli number (cf. Bernoulli numbers).
is the Bernoulli number (cf. Bernoulli numbers).
Comments
References
| [a1] | D.M. Young, R.T. Gregory, "A survey of numerical mathematics" , Dover, reprint (1988) pp. 362ff |
Rectangle rule. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rectangle_rule&oldid=33490