Tricomi equation
A differential equation of the form
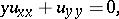 |
which is a simple model of a second-order partial differential equation of mixed elliptic-hyperbolic type with two independent variables 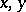 and one open non-characteristic interval of parabolic degeneracy. The Tricomi equation is elliptic for
and one open non-characteristic interval of parabolic degeneracy. The Tricomi equation is elliptic for 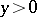 , hyperbolic for
, hyperbolic for 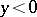 and degenerates to an equation of parabolic type on the line
and degenerates to an equation of parabolic type on the line 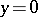 (see [1]). The Tricomi equation is a prototype of the Chaplygin equation
(see [1]). The Tricomi equation is a prototype of the Chaplygin equation
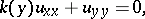 |
where 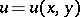 is the stream function of a plane-parallel steady-state gas flow,
is the stream function of a plane-parallel steady-state gas flow, 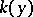 and
and 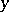 are functions of the velocity of the flow, which are positive at subsonic and negative at supersonic speeds, and
are functions of the velocity of the flow, which are positive at subsonic and negative at supersonic speeds, and  is the angle of inclination of the velocity vector (see [2] [3]).
is the angle of inclination of the velocity vector (see [2] [3]).
Many important problems in the mechanics of continuous media reduce to a boundary value problem for the Tricomi equation, in particular, mixed flows involving the formation of local subsonic zones (see [3], [4]).
References
| [1] | F. Tricomi, "On second-order linear partial differential equations of mixed type" , Moscow-Leningrad (1947) (In Russian; translated from Italian) |
| [2] | S.A. Chaplygin, "On gas-like structures" , Moscow-Leningrad (1949) (In Russian) |
| [3] | F.I. Frankl', "Selected work on gas dynamics" , Moscow (1973) (In Russian) |
| [4] | A.V. Bitsadze, "Some classes of partial differential equations" , Gordon & Breach (1988) (Translated from Russian) |
Comments
See also Tricomi problem and Mixed-type differential equation, for additional references.
References
| [a1] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) |
Tricomi equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tricomi_equation&oldid=33467