One-factor
of a graph
Suppose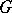 
is a (simple) graph. A matching in 
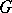is a set of pairwise-disjoint edges in 
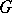. A one-factor or spanning matching is a set of edges such that every vertex of 
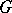occurs in exactly one edge.
Not every graph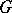 
has a one-factor. One obvious necessary condition is that 
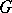has no connected component with an odd number of vertices. However this is not a sufficient condition. The smallest graph connected with an even number of vertices but no one-factor is:
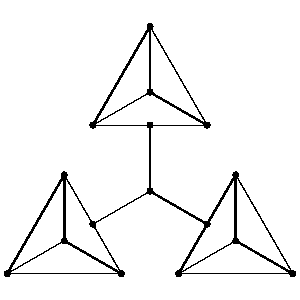
Figure: o110060a
One-factors were first studied by W.T. Tutte, who proved the following characterization. If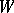 
is any subset of the vertex set 
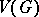of 
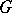, let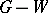 
denote the graph constructed from 
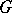by deleting 
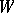and all edges touching members of 
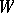. The components of 
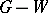are odd or even according as they have an odd or even number of vertices. Write 
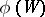for the number of odd components of 
.
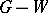Tutte's theorem [a6]: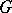 
contains a one-factor if and only if 
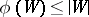whenever 
.
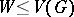A consequence is that for 
even, any regular graph of degree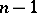 
on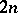 
vertices has a one-factor.
A bridge in a graph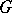 
is an edge whose deletion disconnects 
.
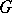Petersen's theorem [a4]: A bridgeless cubic graph contains a one-factor.
This has been generalized by T. Schönberger [a5], who proved that every edge of a bridgeless cubic graph lies in a one-factor. C. Berge [a1] and A.B. Cruse [a3] proved another generalization. If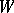 
is any set of vertices of 
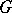, let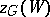 
be the number of edges of 
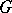with exactly one end-point in 
.
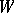The Berge–Cruse theorem: If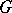 
is a regular graph of degree 
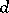with an even number of vertices, and if 
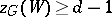for all odd-order subsets 
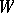of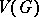 
, then each edge of 
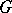belongs to some one-factor.
Consequences are [a3]:
1) if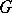 
is a regular graph of degree 
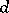with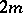 
vertices and 
(
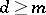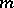odd) or 
(
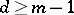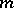even), then every edge of 
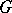belongs to some one-factor;
2) if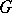 
is a regular graph of valency 
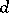with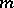 
vertices and 
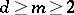, then 
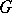contains at least
 |
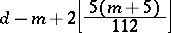disjoint one-factors.
A number of results have been proved concerning whether a graph of a certain description (usually a quite sparse graph) contains a one-factor.
Important references include [a2], and [a7].
References
| [a1] | C. Berge, "Graphs and hypergraphs" , North-Holland (1973) (Translated from French) |
| [a2] | J. Bosák, "Decomposition of graphs" , Kluwer Acad. Publ. (1990) |
| [a3] | A.B. Cruse, "A note on one-factors in certain regular multigraphs" Discrete Math. , 18 (1977) pp. 213–216 |
| [a4] | J. Petersen, "Die Theorie der regulären Graphes" Acta Math. , 15 (1981) pp. 193–220 |
| [a5] | T. Schönberger, "Ein Beweis des Peterschen Graphensatzes" Acta Sci. Math. Szeged , 7 (1934) pp. 51–57 |
| [a6] | W.T. Tutte, "The factorizations of linear graphs" J. London Math. Soc. , 22 (1947) pp. 459–474 |
| [a7] | W.D. Wallis, "One-factorizations" , Kluwer Acad. Publ. (1997) |
One-factor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=One-factor&oldid=33440