Pseudo-character of a set
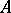in a topological space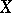 
The smallest infinite cardinal number 
for which there exists a family of cardinality 
of sets open in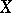 
with intersection 
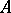. It is usually denoted by 
. The pseudo-character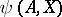 
is defined for all subsets 
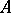of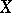 
only when all singleton subsets in 
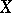are closed. The pseudo-character 
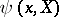of a point 
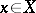in a topological space 
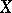is understood to be the pseudo-character 
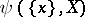of the set 
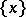in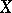 
.
The pseudo-character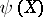 
of a topological space 
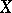is the smallest infinite cardinal number 
such that each point is the intersection of a family of cardinality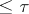 
of sets which are open in 
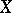. Spaces with countable pseudo-character are those in which every point is a 
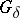-set (cf. Set of type 
(
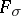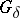)). Each topological space can be represented as the image under a continuous open mapping of a paracompact Hausdorff space with a countable pseudo-character. For compact Hausdorff spaces the countability of the pseudo-character is equivalent to the first axiom of countability. In general, the pseudo-character of a closed set 
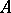in a compact Hausdorff space 
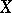is equal to the minimum cardinality of a defining system of neighbourhoods of the set 
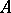in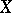 
.
References
| [1] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
| [2] | A.V. Arkhangel'skii, "Classes of topological groups" Russian Math. Surveys , 36 : 3 (1981) pp. 151–174 Uspekhi Mat. Nauk , 36 : 3 (1981) pp. 127–146 |
Comments
References
| [a1] | R. Engelking, "General topology" , Heldermann (1989) |
| [a2] | K. Kunen (ed.) J.E. Vaughan (ed.) , Handbook of set-theoretic topology , North-Holland (1984) pp. Chapts. 1–2 |
Pseudo-character of a set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pseudo-character_of_a_set&oldid=33418