Dehn lemma
Let a three-dimensional manifold  contain a two-dimensional cell
contain a two-dimensional cell  with self-intersections and with a simple closed polygonal curve
with self-intersections and with a simple closed polygonal curve  without singular points as boundary; then there exists a two-dimensional cell
without singular points as boundary; then there exists a two-dimensional cell  with boundary
with boundary  which can be piecewise-linearly imbedded into
which can be piecewise-linearly imbedded into  . Dehn's lemma was introduced in [1], but its proofs contained gaps; for a complete proof see [2]. The following result, known as the loop theorem, is connected with Dehn's lemma: Let
. Dehn's lemma was introduced in [1], but its proofs contained gaps; for a complete proof see [2]. The following result, known as the loop theorem, is connected with Dehn's lemma: Let  be a compact three-dimensional manifold and let
be a compact three-dimensional manifold and let  be a component of its boundary; if the kernel of the homomorphism
be a component of its boundary; if the kernel of the homomorphism  is non-trivial, there exists a simple loop on
is non-trivial, there exists a simple loop on 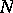 which is not homotopic to zero in
which is not homotopic to zero in  and is homotopic to zero in
and is homotopic to zero in 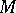 . The loop theorem and Dehn's lemma are usually employed together. They may be combined to yield the following theorem: If
. The loop theorem and Dehn's lemma are usually employed together. They may be combined to yield the following theorem: If  is a three-dimensional manifold with boundary
is a three-dimensional manifold with boundary  and if the kernel of the imbedding homomorphism
and if the kernel of the imbedding homomorphism  is non-trivial, then
is non-trivial, then  contains a piecewise-linearly imbedded two-dimensional disc
contains a piecewise-linearly imbedded two-dimensional disc  , the boundary of which lies in
, the boundary of which lies in  and which is not contractible in
and which is not contractible in  . A related theorem is the sphere theorem which, in conjunction with Dehn's lemma and the loop theorem, is one of the principal tools in the topology of three-dimensional manifolds: If
. A related theorem is the sphere theorem which, in conjunction with Dehn's lemma and the loop theorem, is one of the principal tools in the topology of three-dimensional manifolds: If  is an oriented three-dimensional manifold with
is an oriented three-dimensional manifold with  , then
, then 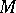 contains a submanifold
contains a submanifold  homeomorphic to a two-dimensional sphere and which is not homotopic to zero in
homeomorphic to a two-dimensional sphere and which is not homotopic to zero in  .
.
These results have numerous applications in the topology of three-dimensional manifolds and, in particular, in knot theory. Thus, if 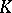 is a knot, then
is a knot, then  is isomorphic to
is isomorphic to 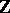 if and only if
if and only if 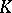 is a trivial knot. The following conditions are equivalent for an
is a trivial knot. The following conditions are equivalent for an  -component link
-component link  in
in  : 1)
: 1)  ; 2)
; 2)  is a free product of two non-trivial groups; and 3)
is a free product of two non-trivial groups; and 3)  contains a submanifold
contains a submanifold  that is homeomorphic to a two-dimensional sphere such that both components of
that is homeomorphic to a two-dimensional sphere such that both components of  contain points from
contain points from  . In particular, if
. In particular, if 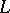 is a knot (i.e.
is a knot (i.e.  ), then
), then  (the theorem on asphericity of knots).
(the theorem on asphericity of knots).
References
| [1] | M. Dehn, "Ueber die Topologie des dreidimensionalen Raumes" Math. Ann. , 69 (1910) pp. 137–168 |
| [2] | C.D. Papakyriakopoulos, "On Dehn's lemma and the asphericity of knots" Ann. of Math. , 66 (1957) pp. 1–26 |
| [3] | J.R. Stallings, "Group theory and three-dimensional manifolds" , Yale Univ. Press (1971) |
Comments
References
| [a1] | W.S. Massey, "Algebraic topology: an introduction" , Springer (1977) |
Dehn lemma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dehn_lemma&oldid=33393