Dehn lemma

Let a three-dimensional manifold contain a two-dimensional cell with self-intersections and with a simple closed polygonal curve without singular points as boundary; then there exists a two-dimensional cell with boundary which can be piecewise-linearly imbedded into . Dehn's lemma was introduced in [1], but its proofs contained gaps; for a complete proof see [2]. The following result, known as the loop theorem, is connected with Dehn's lemma: Let be a compact three-dimensional manifold and let be a component of its boundary; if the kernel of the homomorphism is non-trivial, there exists a simple loop on 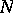which is not homotopic to zero in and is homotopic to zero in 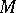. The loop theorem and Dehn's lemma are usually employed together. They may be combined to yield the following theorem: If is a three-dimensional manifold with boundary and if the kernel of the imbedding homomorphism is non-trivial, then contains a piecewise-linearly imbedded two-dimensional disc , the boundary of which lies in and which is not contractible in . 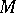A related theorem is the sphere theorem which, in conjunction with Dehn's lemma and the loop theorem, is one of the principal tools in the topology of three-dimensional manifolds: If is an oriented three-dimensional manifold with , then contains a submanifold homeomorphic to a two-dimensional sphere and which is not homotopic to zero in .

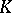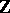These results have numerous applications in the topology of three-dimensional manifolds and, in particular, in knot theory. Thus, if is a knot, then is isomorphic to if and only if 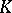is a trivial knot. The following conditions are equivalent for an -component link in : 1) ; 2) is a free product of two non-trivial groups; and 3) contains a submanifold that is homeomorphic to a two-dimensional sphere such that both components of contain points from . 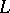In particular, if is a knot (i.e. ), then (the theorem on asphericity of knots).

References

[1]	M. Dehn, "Ueber die Topologie des dreidimensionalen Raumes" Math. Ann. , 69 (1910) pp. 137–168
[2]	C.D. Papakyriakopoulos, "On Dehn's lemma and the asphericity of knots" Ann. of Math. , 66 (1957) pp. 1–26
[3]	J.R. Stallings, "Group theory and three-dimensional manifolds" , Yale Univ. Press (1971)

References

[a1]	W.S. Massey, "Algebraic topology: an introduction" , Springer (1977)