Hedetniemi conjecture

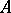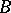For two graphs and (cf. Graph), their categorial product 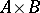is the graph with vertex set 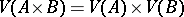while an edge 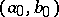is adjacent to an edge 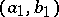if and only if 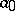is adjacent to and 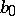is adjacent to 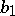. If the graph 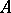has a good -colouring (cf. Graph colouring), then 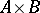has a good -colouring 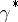, given by 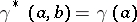. As this statement also holds for good -colourings of 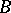, it follows that the chromatic number 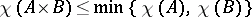. Hedetniemi's conjecture, [a1], is that for all finite graphs 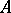and :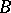

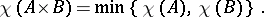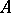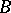The corresponding statement for infinite graphs is not true [a2], but little is known about the relationship between the cardinalities of the chromatic numbers of and and the chromatic number of .

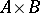It is obvious that the chromatic number of the product of two -chromatic graphs is . L. Lovász [a3] showed that the chromatic number of the product of two -chromatic graphs is and in [a4] it is proven that the chromatic number of the product of two 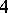-chromatic graphs is 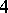. It is not known whether the chromatic number of the product of two -chromatic graphs is always for any 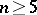. The lack of understanding of this problem is even more embarrassing than that.

Let 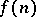be the largest number such that whenever 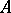and 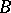are two -chromatic graphs, then the chromatic number of 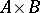is larger than or equal to 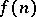. Clearly, if 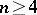, then 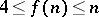and Hedetniemi's conjecture says that 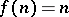. About 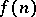it is only known that either 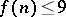for all or 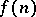is unbounded, [a5] and [a6].

Write if there is a homomorphism from the graph 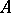to the graph 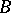(a function from 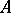to 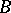which preserves the edges). Write 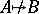if there is no homomorphism from 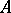to 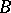. A graph 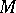is called multiplicative, [a7], [a8], if and imply 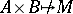. Note that a graph 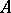has a good -colouring if and only if 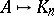. Hence Hedetniemi's conjecture is equivalent to asking whether the complete graph 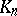(cf. also Graph) is multiplicative.

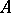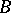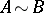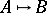Two graphs and are equivalent, , if and 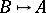. It is not difficult to check that the equivalence classes of finite graphs form a distributive lattice under the order relation and that a graph is multiplicative if and only if it is meet-irreducible in this lattice. Once this general setting of the problem has been realized, it is not difficult to see that Hedetniemi's conjecture has a natural generalization, [a8], to the problem of finding the meet-irreducible elements in the distributive lattices of various types of relational structures. This line of investigation leads to a setting in topos theory and, to a certain extent, in logic, [a9].

Of course this introduces the even more general task of trying to understand the distributive lattice of, say, all finite relational structures of a given type and, in connection with this, the problem of deciding whether there is a homomorphism from a given relational structure to another one of the same type. In this context one of the more interesting types of relational structures are finite directed graphs, [a10]. Multiplicative partially ordered sets have been investigated in [a11].

For graphs, Hedetniemi's conjecture has been confirmed for various special cases and several interesting observations have been made. See [a12], [a13], [a14]. For a general discussion of graph products, see [a15].

References

[a1]	S. Hedetniemi, "Homomorphisms of graphs and automata" Univ. Michigan Technical Report , 03105–44–T (1966)
[a2]	A. Hajnal, "The chromatic number of the product of two 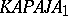-chromatic graphs can be countable" Combinatorica , 5 (1985) pp. 137–140
[a3]	L. Lovász, "Operations with structures" Acta Math. Acad. Sci. Hung. (1967) pp. 321–328
[a4]	M.H. El-Zahar, N.W. Sauer, "The chromatic number of the product of two 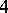-chromatic graphs is " Combinatorica , 5 : 2 (1985) pp. 121–126
[a5]	S. Poljak, "Coloring digraphs by iterated antichains" Comment. Math. Univ. Carolin. , 32 : 2 (1991) pp. 209–212
[a6]	S. Poljak, V. Rödl, "On the arc-chromatic number of a digraph" JCT B , 31 (1981) pp. 190–198
[a7]	D.J. Miller, "The categorical product of graphs" Canad. J. Math. , 20 (1968) pp. 1511–1521
[a8]	R. Haggkvist, P. Hell, D.J. Miller, V.N. Lara, "On multiplicative graphs and the product conjecture" Combinatorica , 8 : 1 (1988) pp. 63–74
[a9]	D. Duffus, N.W. Sauer, "Lattices arising in categorial investigations of Hedetniemi's conjecture" Discrete Math. , 153 (1996)
[a10]	P. Hell, H. Zhou, X. Zhu, "Homomorphisms to oriented cycles" Combinatorica (??)
[a11]	N.W. Sauer, X. Zhu, "Multiplicative posets" Order , 8 (1992) pp. 349–358
[a12]	D. Duffus, B. Sands, R. Woodrow, "On the chromatic number of the product of graphs" J. Graph Th. , 9 (1985) pp. 487–495
[a13]	N.W. Sauer, X. Zhu, "An approach to Hedetniemi's conjecture" J. Graph Th. , 16 : 5 (1992) pp. 423–436
[a14]	G. Sabidussi, "Graph multiplication" Math. Z. , 72 (1960) pp. 446–457
[a15]	R.J. Nowakowski, D. Rall, "Associative graph products and their independence, domination and coloring numbers" J. Graph Th. (??)