Hedetniemi conjecture
For two graphs 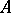 and
and 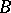 (cf. Graph), their categorial product
(cf. Graph), their categorial product 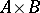 is the graph with vertex set
is the graph with vertex set 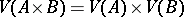 while an edge
while an edge 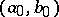 is adjacent to an edge
is adjacent to an edge 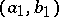 if and only if
if and only if 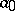 is adjacent to
is adjacent to  and
and 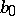 is adjacent to
is adjacent to 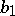 . If the graph
. If the graph 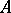 has a good
has a good  -colouring
-colouring 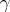 (cf. Graph colouring), then
(cf. Graph colouring), then 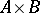 has a good
has a good  -colouring
-colouring 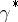 , given by
, given by 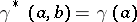 . As this statement also holds for good
. As this statement also holds for good  -colourings of
-colourings of 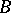 , it follows that the chromatic number
, it follows that the chromatic number 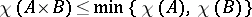 . Hedetniemi's conjecture, [a1], is that for all finite graphs
. Hedetniemi's conjecture, [a1], is that for all finite graphs 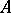 and
and 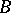 :
:
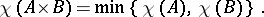 |
The corresponding statement for infinite graphs is not true [a2], but little is known about the relationship between the cardinalities of the chromatic numbers of 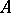 and
and 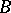 and the chromatic number of
and the chromatic number of 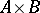 .
.
It is obvious that the chromatic number of the product of two  -chromatic graphs is
-chromatic graphs is  . L. Lovász [a3] showed that the chromatic number of the product of two
. L. Lovász [a3] showed that the chromatic number of the product of two  -chromatic graphs is
-chromatic graphs is  and in [a4] it is proven that the chromatic number of the product of two
and in [a4] it is proven that the chromatic number of the product of two 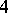 -chromatic graphs is
-chromatic graphs is 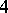 . It is not known whether the chromatic number of the product of two
. It is not known whether the chromatic number of the product of two  -chromatic graphs is always
-chromatic graphs is always  for any
for any 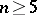 . The lack of understanding of this problem is even more embarrassing than that.
. The lack of understanding of this problem is even more embarrassing than that.
Let 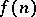 be the largest number such that whenever
be the largest number such that whenever 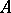 and
and 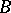 are two
are two  -chromatic graphs, then the chromatic number of
-chromatic graphs, then the chromatic number of 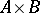 is larger than or equal to
is larger than or equal to 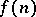 . Clearly, if
. Clearly, if 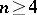 , then
, then 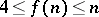 and Hedetniemi's conjecture says that
and Hedetniemi's conjecture says that 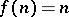 . About
. About 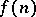 it is only known that either
it is only known that either 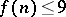 for all
for all  or
or 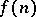 is unbounded, [a5] and [a6].
is unbounded, [a5] and [a6].
Write  if there is a homomorphism from the graph
if there is a homomorphism from the graph 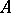 to the graph
to the graph 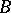 (a function from
(a function from 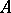 to
to 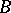 which preserves the edges). Write
which preserves the edges). Write 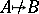 if there is no homomorphism from
if there is no homomorphism from 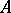 to
to 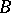 . A graph
. A graph 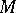 is called multiplicative, [a7], [a8], if
is called multiplicative, [a7], [a8], if  and
and 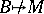 imply
imply 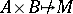 . Note that a graph
. Note that a graph 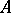 has a good
has a good  -colouring if and only if
-colouring if and only if 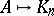 . Hence Hedetniemi's conjecture is equivalent to asking whether the complete graph
. Hence Hedetniemi's conjecture is equivalent to asking whether the complete graph 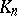 (cf. also Graph) is multiplicative.
(cf. also Graph) is multiplicative.
Two graphs 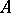 and
and 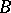 are equivalent,
are equivalent, 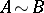 , if
, if 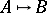 and
and 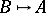 . It is not difficult to check that the equivalence classes of finite graphs form a distributive lattice under the order relation
. It is not difficult to check that the equivalence classes of finite graphs form a distributive lattice under the order relation  and that a graph is multiplicative if and only if it is meet-irreducible in this lattice. Once this general setting of the problem has been realized, it is not difficult to see that Hedetniemi's conjecture has a natural generalization, [a8], to the problem of finding the meet-irreducible elements in the distributive lattices of various types of relational structures. This line of investigation leads to a setting in topos theory and, to a certain extent, in logic, [a9].
and that a graph is multiplicative if and only if it is meet-irreducible in this lattice. Once this general setting of the problem has been realized, it is not difficult to see that Hedetniemi's conjecture has a natural generalization, [a8], to the problem of finding the meet-irreducible elements in the distributive lattices of various types of relational structures. This line of investigation leads to a setting in topos theory and, to a certain extent, in logic, [a9].
Of course this introduces the even more general task of trying to understand the distributive lattice of, say, all finite relational structures of a given type and, in connection with this, the problem of deciding whether there is a homomorphism from a given relational structure to another one of the same type. In this context one of the more interesting types of relational structures are finite directed graphs, [a10]. Multiplicative partially ordered sets have been investigated in [a11].
For graphs, Hedetniemi's conjecture has been confirmed for various special cases and several interesting observations have been made. See [a12], [a13], [a14]. For a general discussion of graph products, see [a15].
References
| [a1] | S. Hedetniemi, "Homomorphisms of graphs and automata" Univ. Michigan Technical Report , 03105–44–T (1966) |
| [a2] | A. Hajnal, "The chromatic number of the product of two 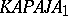 -chromatic graphs can be countable" Combinatorica , 5 (1985) pp. 137–140 -chromatic graphs can be countable" Combinatorica , 5 (1985) pp. 137–140 |
| [a3] | L. Lovász, "Operations with structures" Acta Math. Acad. Sci. Hung. (1967) pp. 321–328 |
| [a4] | M.H. El-Zahar, N.W. Sauer, "The chromatic number of the product of two 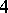 -chromatic graphs is -chromatic graphs is  " Combinatorica , 5 : 2 (1985) pp. 121–126 " Combinatorica , 5 : 2 (1985) pp. 121–126 |
| [a5] | S. Poljak, "Coloring digraphs by iterated antichains" Comment. Math. Univ. Carolin. , 32 : 2 (1991) pp. 209–212 |
| [a6] | S. Poljak, V. Rödl, "On the arc-chromatic number of a digraph" JCT B , 31 (1981) pp. 190–198 |
| [a7] | D.J. Miller, "The categorical product of graphs" Canad. J. Math. , 20 (1968) pp. 1511–1521 |
| [a8] | R. Haggkvist, P. Hell, D.J. Miller, V.N. Lara, "On multiplicative graphs and the product conjecture" Combinatorica , 8 : 1 (1988) pp. 63–74 |
| [a9] | D. Duffus, N.W. Sauer, "Lattices arising in categorial investigations of Hedetniemi's conjecture" Discrete Math. , 153 (1996) |
| [a10] | P. Hell, H. Zhou, X. Zhu, "Homomorphisms to oriented cycles" Combinatorica (??) |
| [a11] | N.W. Sauer, X. Zhu, "Multiplicative posets" Order , 8 (1992) pp. 349–358 |
| [a12] | D. Duffus, B. Sands, R. Woodrow, "On the chromatic number of the product of graphs" J. Graph Th. , 9 (1985) pp. 487–495 |
| [a13] | N.W. Sauer, X. Zhu, "An approach to Hedetniemi's conjecture" J. Graph Th. , 16 : 5 (1992) pp. 423–436 |
| [a14] | G. Sabidussi, "Graph multiplication" Math. Z. , 72 (1960) pp. 446–457 |
| [a15] | R.J. Nowakowski, D. Rall, "Associative graph products and their independence, domination and coloring numbers" J. Graph Th. (??) |
Hedetniemi conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hedetniemi_conjecture&oldid=13925