Riesz summation method
A method for summing series of numbers and functions; denoted by 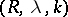 . A series
. A series 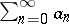 is summable by the Riesz summation method
is summable by the Riesz summation method 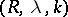 to the sum
to the sum  if
if
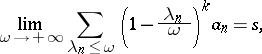 |
where 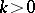 ,
,  , and
, and 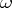 is a continuous parameter. The method was introduced by M. Riesz [1] for the summation of Dirichlet series. The method
is a continuous parameter. The method was introduced by M. Riesz [1] for the summation of Dirichlet series. The method  is regular; when
is regular; when 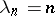 it is equivalent to the Cesàro summation method
it is equivalent to the Cesàro summation method 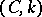 (cf. Cesàro summation methods), and these methods are compatible (cf. Compatibility of summation methods).
(cf. Cesàro summation methods), and these methods are compatible (cf. Compatibility of summation methods).
Riesz considered also a method in which summability of the series 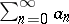 is defined by means of the limit of the sequence
is defined by means of the limit of the sequence 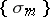 , where
, where
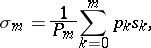 |
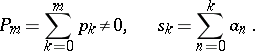 |
This method is denoted by  . The method
. The method 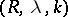 is a modification of the method
is a modification of the method 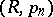 (when
(when 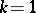 ) and is a generalization of it to the case of an arbitrary
) and is a generalization of it to the case of an arbitrary 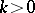 .
.
References
| [1] | M. Riesz, "Une méthode de sommation équivalente à la méthode des moyennes arithmétique" C.R. Acad. Sci. Paris , 152 (1911) pp. 1651–1654 |
| [2] | F. Riesz, "Sur la sommation des séries de Dirichlet" C.R. Acad. Sci. Paris , 149 (1909) pp. 18–21 |
| [3] | G.H. Hardy, M. Riesz, "The general theory of Dirichlet series" , Cambridge Univ. Press (1915) |
| [4] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
Comments
References
| [a1] | K. Zeller, W. Beekmann, "Theorie der Limitierungsverfahren" , Springer (1970) |
Riesz summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riesz_summation_method&oldid=33312