Cubic residue
modulo 
An integer  for which the congruence
for which the congruence 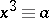 (
( ) is solvable. If the congruence has no solution,
) is solvable. If the congruence has no solution,  is called a cubic non-residue modulo
is called a cubic non-residue modulo 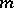 . If the modulus is a prime number
. If the modulus is a prime number  , the congruence
, the congruence 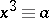 (
(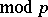 ) may be checked for solvability using Euler's criterion: The congruence
) may be checked for solvability using Euler's criterion: The congruence 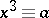 (
(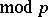 ),
), 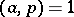 , is solvable if and only if
, is solvable if and only if
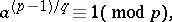 |
where 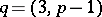 . When the condition is satisfied, the congruence has exactly
. When the condition is satisfied, the congruence has exactly 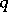 distinct solutions modulo
distinct solutions modulo 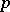 . It follows from the criterion, in particular, that for a prime number
. It follows from the criterion, in particular, that for a prime number  , the sequence of numbers
, the sequence of numbers  contains exactly
contains exactly 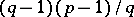 cubic non-residues and
cubic non-residues and 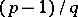 cubic residues modulo
cubic residues modulo 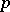 .
.
Comments
From class field theory one obtains, e.g., that  is a cubic residue modulo a prime number
is a cubic residue modulo a prime number 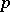 if and only if
if and only if 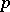 can be written in the form
can be written in the form 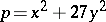 with integers
with integers  and
and  . See also Quadratic residue; Reciprocity laws; Complete system of residues; Reduced system of residues.
. See also Quadratic residue; Reciprocity laws; Complete system of residues; Reduced system of residues.
Cubic residue. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cubic_residue&oldid=33285