Neutral differential equation

A differential equation with distributed argument (cf. Differential equations, ordinary, with distributed arguments) in which the highest derivative occurs for more than one value of the argument, among them a basic (untransformed) one, and this latter value is the largest of those present in the equation. For example, the equation

(*)

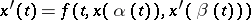is a neutral differential equation when , .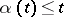

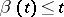For a neutral differential equation the initial value problem is solvable; thus, if for (*) with increasing 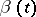one gives

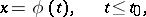then for

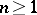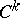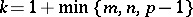there exists a (for unique) piecewise-smooth solution, which belongs to when compatibility conditions hold, that is, conditions of the type

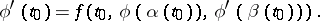Neutral differential equations are one of the most thoroughly studied classes of equations with distributed arguments. They occur naturally in applied problems that contain in their statement some recurrence property.

References

[a1]	J.K. Hale, "Theory of functional differential equations" , Springer (1977) pp. Chapt. 12