Hyperbolic group
in the sense of Gromov, Gromov hyperbolic group
A group  with a finite generating subset
with a finite generating subset  for which there is some constant
for which there is some constant 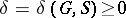 such that
such that
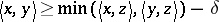 |
for all  , where
, where  and
and 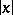 is the smallest integer
is the smallest integer  such that
such that  can be written as a product of
can be written as a product of  elements in
elements in  .
.
Hyperbolic groups are sometimes called word hyperbolic groups or negatively curved groups.
A finite group is a trivial example of a hyperbolic group. Free groups of finite rank (cf. Free group) and fundamental groups of compact Riemannian manifolds of negative sectional curvature (cf. Fundamental group; Riemannian manifold) are hyperbolic. Groups given by a finite presentation satisfying the  small-cancellation condition are also hyperbolic. The free product of two hyperbolic groups is a hyperbolic group. If
small-cancellation condition are also hyperbolic. The free product of two hyperbolic groups is a hyperbolic group. If  is a group and
is a group and  is a subgroup of finite index, then
is a subgroup of finite index, then  is hyperbolic if and only if
is hyperbolic if and only if  is hyperbolic. Algebraic properties of hyperbolic groups can be obtained via geometric methods. Every hyperbolic group is finitely presented (cf. Finitely-presented group), has a solvable word problem and even a solvable conjugacy problem. If
is hyperbolic. Algebraic properties of hyperbolic groups can be obtained via geometric methods. Every hyperbolic group is finitely presented (cf. Finitely-presented group), has a solvable word problem and even a solvable conjugacy problem. If  is a hyperbolic group with a fixed generating subset
is a hyperbolic group with a fixed generating subset  and if
and if  denotes the number of elements
denotes the number of elements  such that
such that  , then the growth function
, then the growth function 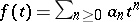 is rational (cf. Polynomial and exponential growth in groups and algebras). Every hyperbolic group is automatic in the sense of [a1]. A hyperbolic group is said to be elementary if it is finite or contains an infinite cyclic subgroup of finite index. Every non-elementary hyperbolic group contains a free subgroup of rank
is rational (cf. Polynomial and exponential growth in groups and algebras). Every hyperbolic group is automatic in the sense of [a1]. A hyperbolic group is said to be elementary if it is finite or contains an infinite cyclic subgroup of finite index. Every non-elementary hyperbolic group contains a free subgroup of rank  . Torsion-free hyperbolic groups (cf. Group without torsion) have finite cohomological dimension. It is not known (1996) whether every hyperbolic group admits a torsion-free subgroup of finite index.
. Torsion-free hyperbolic groups (cf. Group without torsion) have finite cohomological dimension. It is not known (1996) whether every hyperbolic group admits a torsion-free subgroup of finite index.
See also Gromov hyperbolic space.
References
| [a1] | D.B.A. Epstein, J.W.W. Cannon, D.F. Holt, S.V.F. Levy, M.S. Paterson, W.P. Thurston, "Word processing in groups" , Bartlett and Jones (1992) |
| [a2] | M. Coornaert, T. Delzant, A. Papadopoulos, "Géométrie et théorie des groupes: les groupes hyperboliques de Gromov" , Lecture Notes in Mathematics , 1441 , Springer (1991) |
| [a3] | "Sur les groupes hyperboliques d'après Mikhael Gromov" E. Ghys (ed.) P. de la Harpe (ed.) , Progress in Maths. , 83 , Birkhäuser (1990) |
| [a4] | M. Gromov, "Hyperbolic groups" S.M. Gersten (ed.) , Essays in Group Theory , MSRI Publ. , 8 , Springer (1987) pp. 75–263 |
Hyperbolic group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_group&oldid=33250