Quasi-norm
A non-negative function 
defined on a linear space 
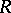and satisfying the same axioms as a norm except for the triangle inequality 
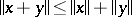, which is replaced by the weaker requirement: There exists a constant 
such that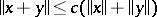 
for all 
.
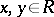Comments
The topology of a locally bounded topological vector space can be given by a quasi-norm. Conversely, a quasi-normed vector space is locally bounded. Here a set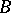 
in a topological vector space is bounded if for each open neighbourhood 
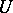of zero there is a 
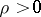such that 
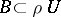, and a topological vector space is locally bounded if there is a bounded neighbourhood of zero. Given a circled bounded neighbourhood 
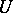of zero in a topological vector space 
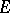(a set 
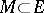is circled if 
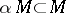for all 
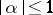), the Minkowski functional of 
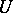is defined by 
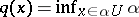. It is a quasi-norm.
References
| [a1] | G. Köthe, "Topological vector spaces" , 1 , Springer (1969) pp. 159 |
Quasi-norm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-norm&oldid=33232