Infinitely-large function
From Encyclopedia of Mathematics
A function of a variable 
whose absolute value becomes and remains larger than any given number as a result of variation of 
. More exactly, a function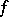 
defined in a neighbourhood of a point 
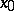is called an infinitely-large function as 
tends to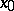 
if for any number 
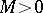it is possible to find a number 
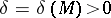such that for all 
satisfying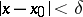 
the inequality 
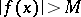holds. This fact may be written as follows:
 |
The following are defined in a similar manner:
 |
 |
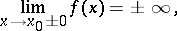For example,
 |
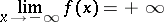means that for any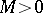 
it is possible to find a 
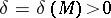such that the inequality 
is valid for all 
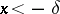. The study of infinitely-large functions may be reduced to that of infinitely-small functions (cf. Infinitely-small function), since 
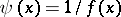will be infinitely small.
Comments
See also Infinitesimal calculus.
How to Cite This Entry:
Infinitely-large function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Infinitely-large_function&oldid=33180
Infinitely-large function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Infinitely-large_function&oldid=33180
This article was adapted from an original article by V.I. Bityutskov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article