Approximation in the mean
From Encyclopedia of Mathematics
Approximation of a given function 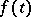 , integrable on an interval
, integrable on an interval 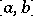 , by a function
, by a function 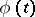 , where the quantity
, where the quantity
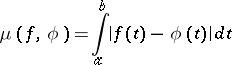 |
is taken as the measure of approximation.
The more general case, when
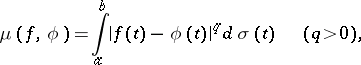 |
where 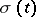 is a non-decreasing function different from a constant on
is a non-decreasing function different from a constant on 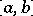 , is called mean-power approximation (with exponent
, is called mean-power approximation (with exponent 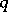 ) with respect to the distribution
) with respect to the distribution 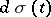 . If
. If 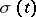 is absolutely continuous and
is absolutely continuous and 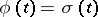 , then one obtains mean-power approximation with weight
, then one obtains mean-power approximation with weight 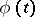 , and if
, and if 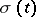 is a step function with jumps
is a step function with jumps 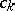 at points
at points 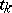 in
in 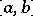 , one has weighted mean-power approximation with respect to the system of points
, one has weighted mean-power approximation with respect to the system of points 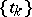 with measure of approximation
with measure of approximation
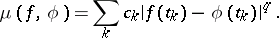 |
These concepts are extended in a natural way to the case of functions of several variables.
References
| [1] | V.L. Goncharov, "The theory of interpolation and approximation of functions" , Moscow (1954) (In Russian) |
| [2] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
| [3] | J.R. Rice, "The approximation of functions" , 1. Linear theory , Addison-Wesley (1964) |
Comments
References
| [a1] | A.F. Timan, "Theory of approximation of functions of a real variable" , Pergamon (1963) (Translated from Russian) |
| [a2] | T.J. Rivlin, "An introduction to the approximation of functions" , Dover, reprint (1981) |
| [a3] | E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982) pp. 203ff |
How to Cite This Entry:
Approximation in the mean. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximation_in_the_mean&oldid=33102
Approximation in the mean. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximation_in_the_mean&oldid=33102
This article was adapted from an original article by N.P. KorneichukV.P. Motornyi (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article