Integral ideal
From Encyclopedia of Mathematics
An ideal of the field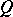 
relative to a ring 
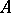(here 
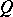is the field of fractions of 
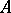, cf. Fractions, ring of) that lies entirely in 
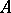. An integral ideal is an ideal in 
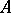, and, conversely, every ideal of 
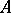is an integral ideal of the field of fractions 
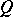of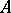 
.
Comments
An ideal of the field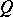 
relative to a ring 
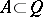is an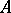 
-submodule of the 
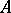-module 
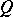. These are also called fractional ideals, cf. Fractional ideal.
References
| [a1] | E. Weiss, "Algebraic number theory" , McGraw-Hill (1963) |
How to Cite This Entry:
Integral ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_ideal&oldid=33086
Integral ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_ideal&oldid=33086
This article was adapted from an original article by O.A. Ivanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article