Centre of a topological dynamical system

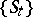(of a flow (continuous-time dynamical system) or of a cascade) with phase space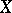

The largest closed invariant set 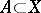for which all points are non-wandering (cf. Non-wandering point) under the restriction of the original system to 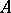. (Cf. also Topological dynamical system.) The centre is necessarily non-empty if the space 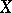is compact (more generally, if there is a semi-trajectory with compact closure). G.D. Birkhoff, who introduced the concept of a centre, used another, but equivalent, definition by means of a certain transfinite process (see [1]–[4]). The number of steps of this process is called the depth of the centre (in fact, there are several "depths" , since this process allows certain modifications). The depth of the centre is not large for flows on compact manifolds of dimension 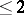(see [5], [6]) or for cascades obtained by the iteration of a homeomorphism of a circle or of an (even non-invertible) continuous mapping of an interval (see [7]), but it can be an arbitrarily large countable transfinite number even for flows in 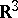and on certain open surfaces (see [8]–[10]). In a complete metric space the centre coincides with the closure of the set of points having the property of Poisson stability.

If 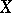is compact and 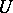is a neighbourhood of the centre, then the trajectory of each point 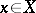"stays most of the time in U" : The fraction in 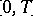of those 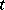for which 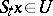tends to 1 as 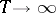. However, the smallest closed invariant set having this property (the minimal centre of attraction, see [3] and [4]) is, in general, only a part of the centre; in the metrizable case it coincides with the closure of the union of all ergodic sets (cf. Ergodic set).

References

[1]	G.D. Birkhoff, "Ueber gewisse Zentralbewegungen dynamischer Systeme" Nachr. Gesells. Wiss. Göttingen Math. Phys. Kl. : 1 (1926) pp. 81–92 (Collected Math. Papers, Vol. II, pp. 283–294)
[2]	G.D. Birkhoff, "Dynamical systems" , Amer. Math. Soc. (1927)
[3]	V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian)
[4]	K.S. Sibirskii, "Introduction to topological dynamics" , Noordhoff (1975) (Translated from Russian)
[5]	A.F. Schwartz, E.S. Thomas, "The depth of the centre of 2-manifolds" , Global stability , Proc. Symp. Pure Math. , 14 , Amer. Math. Soc. (1970) pp. 253–264
[6]	D.A. Neumann, "Central sequences in flows on 2-manifolds of finite genus" Proc. Amer. Math. Soc. , 61 : 1 (1976) pp. 39–43
[7]	O.M. Sharkov'skii, "Fixed points and the centre of a continuous mapping of the line into itself" Dopov. Akad. Nauk. Ukr.RSR , 7 (1964) pp. 865–868 (In Russian) (English summary)
[8]	A.G. Maier, "On central trajectories and a problem of Birkhoff" Mat. Sb. , 26 : 2 (1950) pp. 265–290 (In Russian)
[9]	L.P. Shil'nikov, "On the work of A.G. Maier on central motions" Math. Notes , 5 : 3 (1969) pp. 204–206 Mat. Zametki , 5 : 3 (1969) pp. 335–339
[10]	D.A. Neumann, "Central sequences in dynamical systems" Amer. J. Math. , 100 : 1 (1978) pp. 1–18