Linear topology

on a ring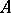

A topology on a ring for which there is a fundamental system of neighbourhoods of zero consisting of left ideals (in this case the topology is said to be left linear). Similarly, a topology on a left 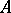-module 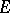is linear if there is a fundamental system of neighbourhoods of zero consisting of submodules. The most extensively used is the adic topology, a basis of which is given by the powers of an ideal.

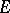A separable linearly topologized -module is called a linearly-compact module if any filter basis (cf. Filter) consisting of affine linear varieties of 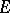(that is, subsets of the form 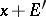, where and 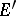is a submodule of 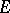) has a limit point. Any module of finite type over a complete local Noetherian ring is linearly compact.

References

[1]	N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French)

Comments

Gabriel topologies on rings are examples of linear topologies; these appear in the theory of localization (cf. Localization in a commutative algebra) or torsion theory. Gabriel topologies correspond to Serre localizing subcategories of the category of left modules over the ring.

References

[a1]	J.S. Golan, "Localization of noncommutative rings" , M. Dekker (1975)
[a2]	B. Stenström, "Rings of quotients" , Springer (1975)
[a3]	F. Van Oystaeyen, A. Verschoren, "Reflectors and localization. Application to sheaf theory" , M. Dekker (1979)
[a4]	J. Lambek, "Torsion theories, additive semantics and rings of quotients" , Lect. notes in math. , 77 , Springer (1971)