Kummer hypothesis
From Encyclopedia of Mathematics
A hypothesis concerning the behaviour of the cubic Gauss sum
 |
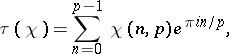where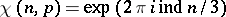 
is a cubic character modulo 
(
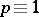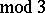) and 
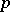is a prime number. It is known that
 |
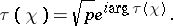Therefore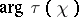 
lies either in the first, third or fifth sextant. Accordingly, E. Kummer divided all primes 
(
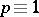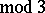) into three classes, 
, 
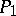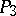and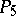 
. The Kummer hypothesis is that each of the classes 
, 
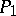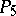and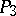 
contains infinitely many primes, and that their respective asymptotic densities are 
, 
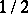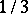and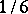 
. There are various generalizations of the Kummer hypothesis to characters of order higher than 3. A modified version of the hypothesis has been proved (see [3]).
References
| [1] | H. Hasse, "Vorlesungen über Zahlentheorie" , Springer (1950) |
| [2] | H. Davenport, "Multiplicative number theory" , Springer (1980) |
| [3] | D.R. Heath-Brown, S.I. Patterson, "The distribution of Kummer sums at prime arguments" J. Reine Angew. Math. , 310 (1979) pp. 111–130 |
How to Cite This Entry:
Kummer hypothesis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kummer_hypothesis&oldid=32762
Kummer hypothesis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kummer_hypothesis&oldid=32762
This article was adapted from an original article by B.M. Bredikhin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article